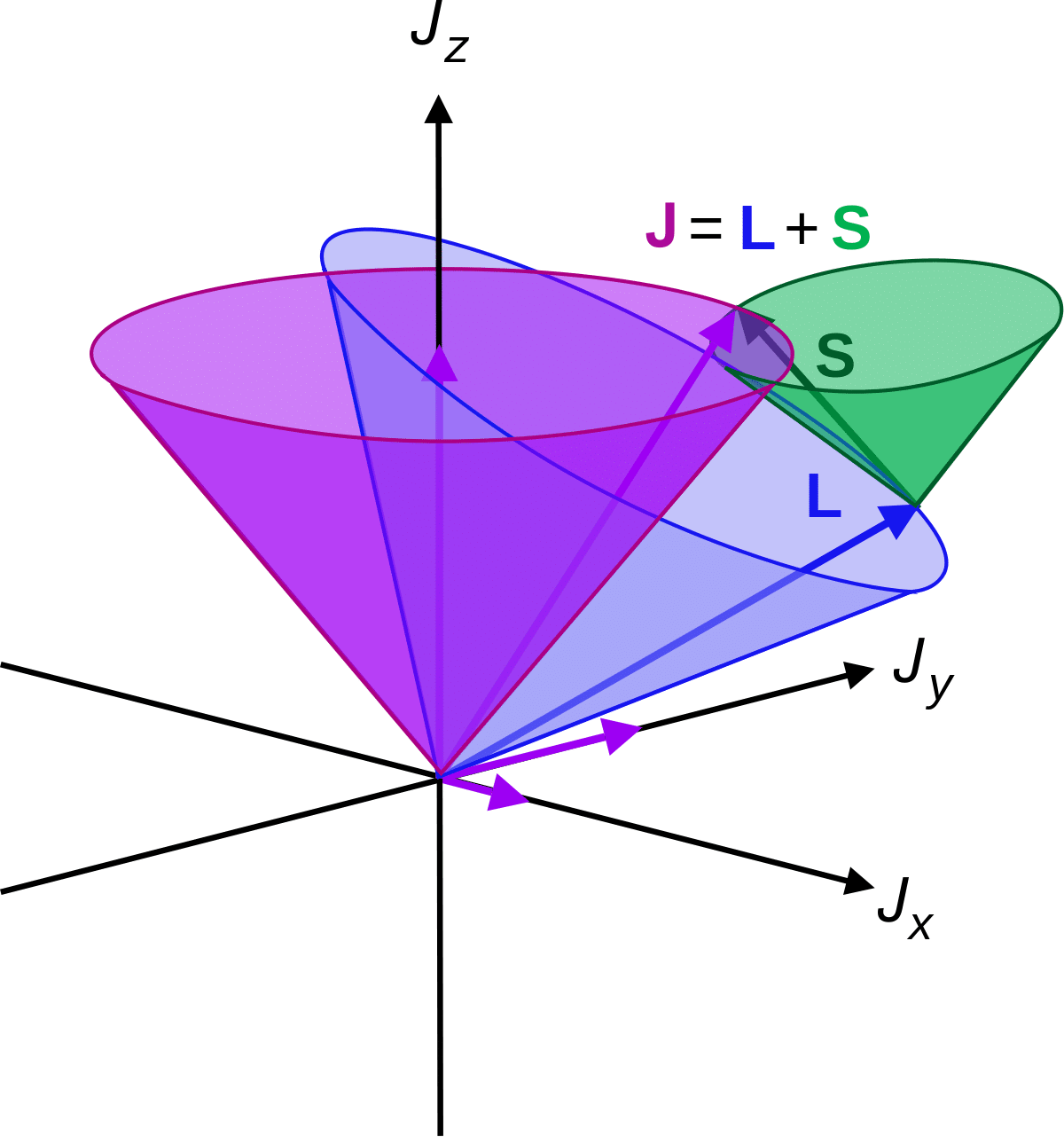
Në fizikë, vrulli studiohet si vrulli këndor. Kjo sasi e lëvizjes këndore zbatohet në lëvizjen rrotulluese, e cila bën që vrulli të jetë për lëvizjen përkthyese. Momenti këndor është një sasi vektoriale që karakterizohet kryesisht nga rrotullimi i një grimce në një mënyrë të përpiktë ose një objekti të shtrirë rreth një boshti që kalon përmes një pike.
Në këtë artikull ne do t'ju tregojmë gjithçka që duhet të dini rreth momentit këndor të dobisë së tij në fizikë.
Çfarë është momenti këndor

Kur përpiqemi ta llogarisim atë për ndonjë objekt që ndodhet lëvizja rreth një boshti është gjithmonë e nevojshme të specifikojmë boshtin e rrotullimit në mënyrë të përshtatshme. Ne do të fillojmë të matim me një pikë materiale të masës m, momenti këndor është shkruar nga shkurtesa L. Impulsi linear është p dhe pozicioni i grimcës në lidhje me boshtin që kalon përmes një pike të caktuar O është r.
Kështu kemi që llogaritet si më poshtë: L = rxp
Reaktori që rezulton nga një produkt vektorial është pingul me planin që formohet nga vektorët pjesëmarrës. Kjo do të thotë se drejtimi kuptimi që mund të gjendet nga rregulli i dorës së djathtë për produktin kryq. Impulsi këndor matet në njësi kg për metër katror / sekondë. Kjo matet sipas sistemit ndërkombëtar të njësive dhe nuk ka ndonjë emër të veçantë.
Ky përkufizim i momentit këndor ka kuptimin më të madh për trupat që përbëhen nga shumë grimca.
Sasia e lëvizjes këndore

Ne përdorim momentin këndor të një grimce pikë për të karakterizuar gjendjen e rrotullimit të një pike ose një trupi që mund të trajtohet si i tillë. Mos harroni se kjo ndodh kur dimensionet e trupit janë të papërfillshme në krahasim me trajektoren e lëvizjes së tij. Në lidhje me vektorët e momentit këndor në lidhje me një pikë të caktuar dhe momentit linear të një grimce pikë që lëviz pasi perimetri është momenti këndor.
Për rastin e një grimce që lëviz në një perimetër, këndi është 90 gradë. Kjo sepse shpejtësia e momentit këndor është gjithmonë tangjente me perimetrin dhe për këtë arsye pingul me rrezen.
Kur flasim për momentin këndor flasim edhe për momentin e inercisë. Kjo nuk është asgjë më shumë sesa ajo që përshkruhet kur një trup i ngurtë ka një inerci të trupit të tij kundër rrotullimit rreth një boshti të caktuar. Ky moment i inercisë varet jo vetëm nga masa e trupit, por edhe nga distanca nga vetë trupi në boshtin e rrotullimit. Kjo mund të kuptohet më lehtë nëse mendojmë se, për disa objekte, është më e lehtë të rrotullohen në lidhje me të tjerët në të njëjtin aks. Kjo varet nga formimi dhe struktura e vetë objektit.
Për një sistem grimcash momenti i inercisë shënohet me shkronjën I dhe llogaritet nga formula e mëposhtme:
Unë = ∑ ri2 Δmi
Këtu kemi që fama e saj me m është një pjesë e vogël e masës dhe r është distanca që trupi ka në lidhje me boshtin e rrotullimit. Trupi do të zgjatet plotësisht dhe do të përbëhet nga grimca të shumta, prandaj momenti i tij i përgjithshëm i inercisë është shuma e të gjitha produkteve midis masës dhe distancës. Varet nga gjeometria që ata kanë, përmbledhja ndryshon dhe kalon nga një integrale në një diferenciale. Koncepti i momentit të inercisë është i lidhur ngushtë me momentin këndor të një objekti ose plotësisht të zgjatur.
Momenti këndor i një sistemi grimcash

Ne do të shqyrtojmë një sistem të grimcave që është i përbërë nga masa të ndryshme dhe që rrotullohet duke ndjekur një perimetër në të njëjtën kohë në planin xy, secila prej tyre ka një shpejtësi lineare që lidhet me shpejtësinë këndore. Në këtë mënyrë, totali i sistemit mund të llogaritet dhe jepet nga përmbledhja e mëposhtme:
L = ω ∑ri2 Δmi
Një trup i zgjatur mund të ndahen në feta secila me një moment tjetër këndor. Nëse boshti i simetrisë së objektit në fjalë përkon me boshtin z nuk ka problem. Dhe kjo sepse ka pika që nuk janë në rrafshin xy, kështu që përbërësit që e formojnë atë dhe që janë pingul me boshtin në fjalë anulohen.
Le të shohim tani kur ndryshon. Normalisht, kur një forcë neto vjen të veprojë kundër një trupi ose një grimce, vrulli i kësaj të veçantë mund të ndryshojë. Si pasojë, po kështu do të jetë edhe vrulli këndor.
Nga ana tjetër, ruajtja ndodh kur ndryshon matësin ekzistues të momentit rrotullues. Nëse ai çift rrotullues është zero, momenti këndor ruhet vazhdimisht. Ky rezultat është ende i vlefshëm edhe në rast se trupi nuk është plotësisht i ngurtë.
Shembuj të momentit këndor
E gjithë kjo ka qenë shumë teori dhe nuk mund të kuptohet mirë pa shembuj praktikë. Le të shohim shembuj praktikë të momentit këndor. Në të parën kemi patinazh artistik dhe sporte të tjera ku ka kthesa. Kur një patinator fillon të kthehet, ajo shtrin krahët dhe më pas na përqafon në trupat tanë për të kryqëzuar këmbët. Kjo është bërë për të rritur shpejtësinë e kthimit. Kurdoherë që trupi lëkundet vazhdimisht, ai tkurret. Falë kësaj tkurrjeje mund të rrisë shpejtësinë e rrotullimit. Kjo për faktin se fakti i aftësisë për të kontraktuar krahët dhe këmbët gjithashtu zvogëlon momentin e inercisë. Meqenëse momenti këndor është i ruajtur, shpejtësia këndore rritet.
Një shembull tjetër është pse macet ulen në këmbë. Megjithëse nuk ka një lëvizje fillestare, sigurohet që shpejt të thuhen si këmbët, ashtu edhe bishti për të ndryshuar inercinë e rrotullimit dhe për të rënë nga këmba. Ndërsa ata manovrojnë që kthehen, vrulli këndor i tyre është zero pasi rrotullimi i tyre nuk është i vazhdueshëm.
Unë shpresoj që me këtë informacion të mund të mësoni më shumë rreth tij.