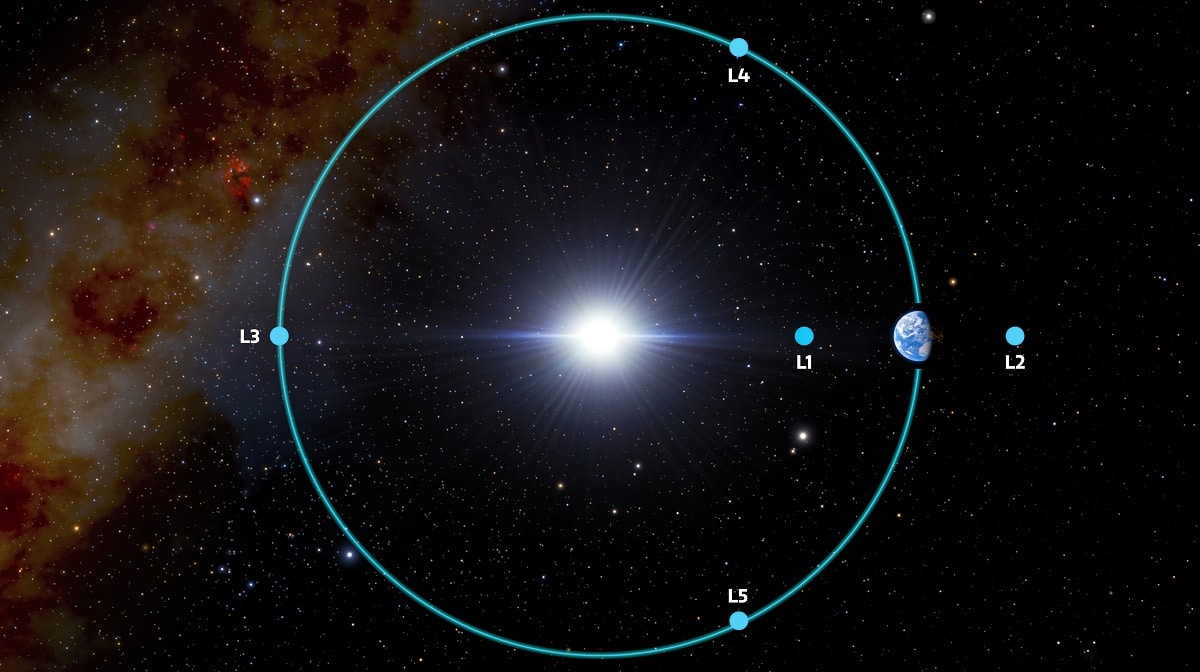
Vidste du, at der er punkter i et objekts kredsløb omkring et andet objekt, hvor vi kan placere en satellit eller et andet himmellegeme, der kan glide hen over det og forblive i rummet, altid i samme afstand fra begge objekter? Dette er kendt som Lagrangiske punkter Og de er mere nyttige, end du troede.
Derfor vil vi dedikere denne artikel til at fortælle dig, hvad Lagrange-punkter er, deres egenskaber og vigtighed.
Hvad er Lagrange-punkter?

Lagrangepunkter er en manifestation af den himmelske mekanik. De modtager deres navn til ære for den franske matematiker Joseph-Louis Lagrange, som opdagede og studerede dem i dybden i det XNUMX. århundrede. Disse specielle punkter findes i systemet dannet af to legemer, der kredser om et tredje legeme, såsom en planet og dens måne, eller en planet og Solen.
Forestil dig, at du har to kroppe, den ene større end den anden, der drejer rundt om et centralt punkt, som Solen. Nå, Lagrange-punkterne er specifikke steder i denne konfiguration, hvor tyngdekraften af de to kroppe balancerer lige meget. På en meget speciel måde. Med andre ord, på disse punkter udlignes centrifugalkraften og gravitationskraften, og det skaber en slags "hvilepunkt" i rummet.
Men hvor er disse punkter helt præcist? Godt, der er fem Lagrange-punkter i alt, nummereret L1 til L5. Punkt L1 er placeret mellem de to legemer i kredsløb, på den samme imaginære linje, som forbinder dem. Punkt L2 er på sin side på samme linje, men på den modsatte side af L1. Punkterne L3, L4 og L5 danner en ligesidet trekant med de to legemer i kredsløb, hvor L3 er punktet modsat det mere massive legeme, og L4 og L5 er placeret henholdsvis foran og bagved dette legeme.
Detaljeret beskrivelse
L1
Jo tættere en genstand er på solen (eller på de genstande, den omgiver), jo hurtigere bevæger den sig. På denne måde vil satellitter med kredsløb mindre end Jordens kredsløb nå Jorden før eller siden. Men hvis vi sætter det i midten, Jordens tyngdekraft er rettet i den modsatte retning af solens tyngdekraft, og udligner noget af solens skub, får den til at kredse med en langsommere hastighed. Hvis afstanden er korrekt, vil satellitten rejse langsomt nok til at bevare sin position mellem jorden og solen. Dette er L1-punktet, der vil blive brugt til at overvåge Solens overflade, da partikelstråler derfra når L1 en time før de når vores planet.
L2
Det samme, der skete med L1, sker på den anden side af Jorden, ud over vores bane. ELLEREt rumfartøj placeret der ville være længere væk fra solen, end vi er, og ville ende med at halte bagud., men i den korrekte afstand ville solens tyngdekraftspåvirkning føje til jordens og få satellitterne til at kredse om jorden.
L3
L3 er på den anden side af solen, lidt bag vores planets kredsløb. Objekter i L3 kan aldrig observeres fra Jorden. Faktisk bruges dette punkt ofte i science fiction til at lokalisere planeter, der deler vores kredsløb. Dette er mindre stabilt end L1 eller L2. Enhver forstyrrelse vil få rumfartøjet, satellitten eller sonden til at bevæge sig væk fra det, hvilket kræver konstant brug af motorerne for at blive i det rigtige område. Dette sker dybest set, fordi andre planeter er tættere på det punkt end vores planet. For eksempel, Venus passerer omkring 50 km fra punkt L000 hver 000. måned.
L4 og L5
Punkterne L4 og L5 er placeret 60 grader foran og bagved Jorden set fra Solen, tæt på Jordens bane. I modsætning til resten er L4 og L5 meget modstandsdygtige over for enhver gravitationsforstyrrelse. Af denne grund har støv og asteroidemateriale tendens til at samle sig i disse områder.
Vigtigheden af Lagrange-punkter
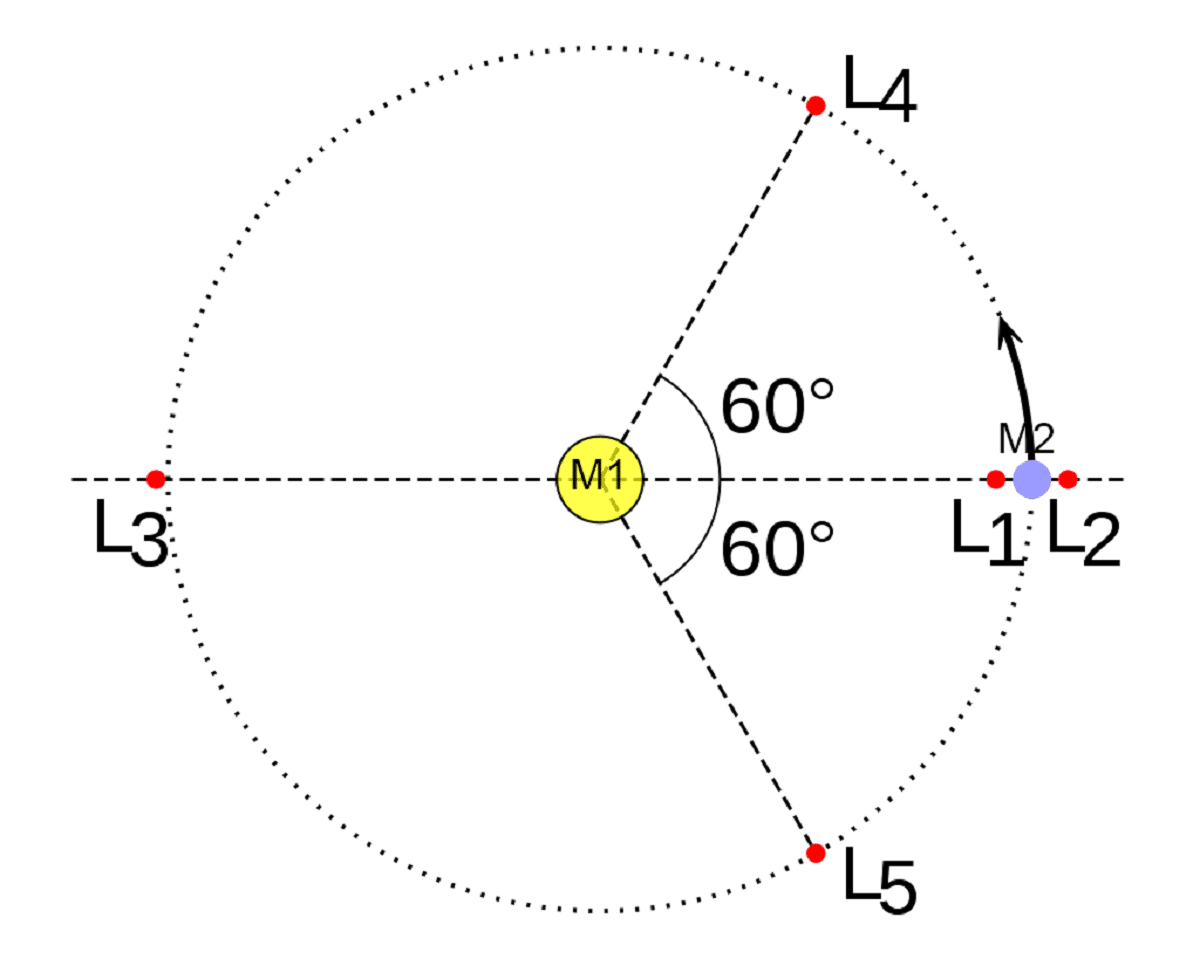
Disse Lagrange-punkter er specielle steder, fordi enhver lille genstand placeret på dem vil forblive stabil i forhold til de to kredsende legemer. Det betyder, at en satellit eller et rumfartøj kunne opholde sig på et af disse punkter uden konstant at bruge thrustere. Det er derfor Lagrange peger de er af stor interesse for rumudforskning og placering af satellitter i rummet.
Ud over deres praktiske anvendelighed har Lagrange-punkter også teoretisk betydning i studiet af himmelmekanik og dynamikken i systemer af kredsende legemer. Deres opdagelse og forståelse har gjort det muligt for os have en mere fuldstændig og præcis vision af stjernernes bevægelse i rummet.
Den virkelige betydning af Lagrange-punkter overskrider deres blotte praktiske anvendelighed i rumudforskning og satellitplacering. Disse punkter repræsenterer et fascinerende vindue til forståelsen af adfærden af dynamiske systemer i rummet og giver os mulighed for at studere komplekse fænomener inden for himmelfysik.
Anvendelser og applikationer
En af de mest bemærkelsesværdige anvendelser af Lagrange-punkter er stabiliteten af satellitter i kredsløb. Ved at placere en satellit på et af disse punkter kan vi holde den praktisk talt stationær i forhold til Jorden eller ethvert andet legeme i systemet. Dette er især nyttigt til jordobservationsmissioner, hvor der kræves en fast position for at få detaljerede billeder af en specifik region over lange perioder.
Derudover giver Lagrange-punkterne også mulighed for at etablere "konstellationer" af satellitter i kredsløb om et himmellegeme. Disse konstellationer kan bruges til en række forskellige formål, som f.eks global kommunikation, klimaovervågning, astronomisk observation og udforskning af rummet. Ved at distribuere satellitterne på forskellige Lagrange-punkter kan vi optimere dækningen og effektiviteten af vores rummissioner.
Et andet område, hvor de er af stor relevans, er i undersøgelsen og udforskningen af asteroider og kometer. Disse punkter fungerer som strategiske steder til at lokalisere rumsonder, der ønsker at studere disse himmellegemer i detaljer. Ved at opholde sig ved et Lagrange-punkt tæt på en asteroide eller komet, kan sonderne undersøge dens sammensætning, struktur og adfærd uden at skulle forbruge store mængder brændstof for at opretholde en stabil bane.
Jeg håber, at du med denne information kan lære mere om Lagrange-punkter, deres egenskaber og anvendelser.