Kutni zamah

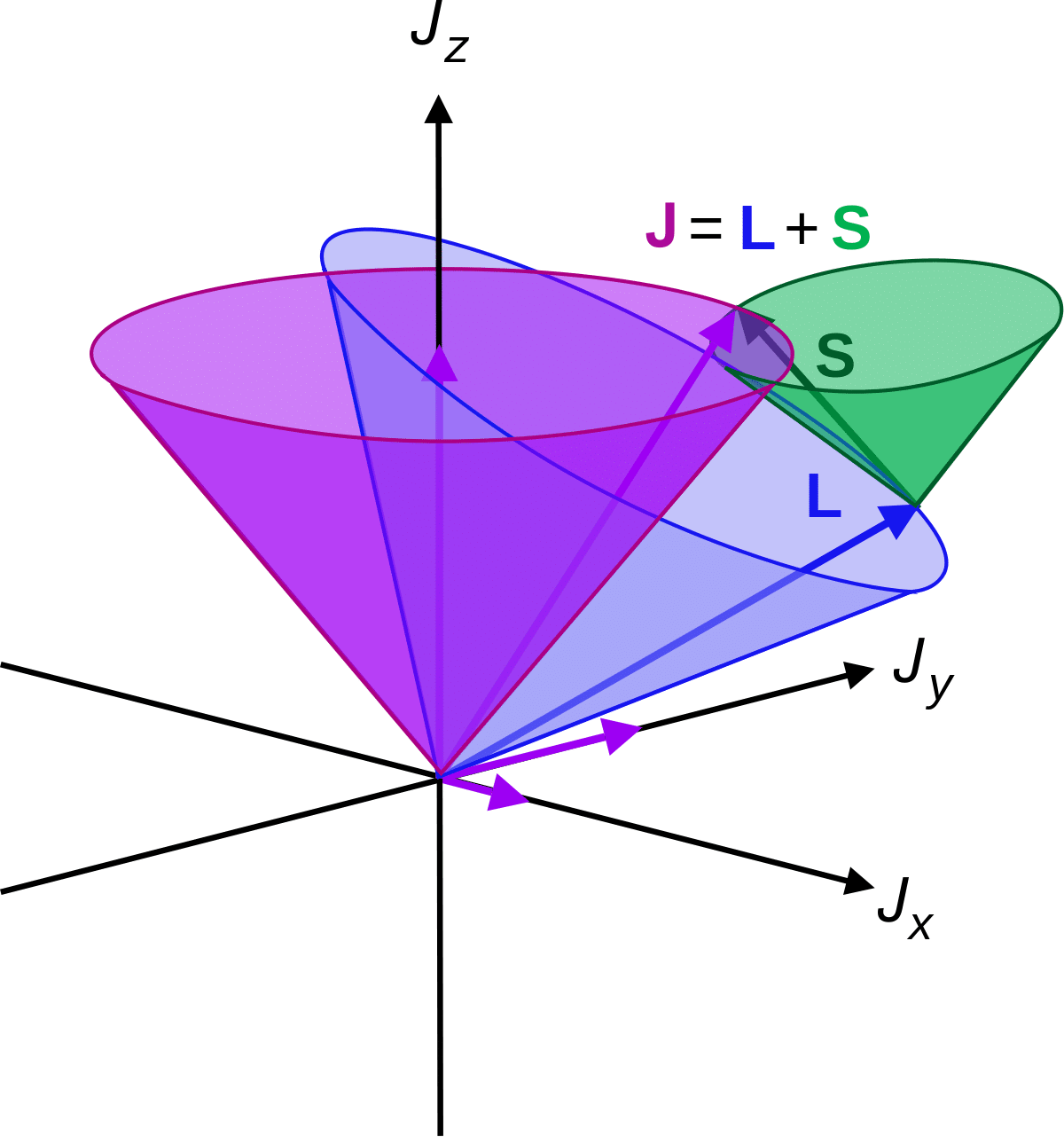
U fizici se zamah proučava kao kutni moment. Ova količina kutnog kretanja primjenjuje se u rotacijskom kretanju, što čini zamah translacijskog gibanja. Kutni impuls je vektorska veličina koja se uglavnom karakterizira rotacijom čestice na tačan način ili predmeta koji se proteže oko osi koja prolazi kroz tačku.

U ovom članku ćemo vam reći sve što trebate znati o kutnom momentu njegove korisnosti u fizici.

Šta je kutni moment

Kada pokušavamo izračunati neki objekt koji se nalazi u pokretu oko osi, uvijek je potrebno zgodno odrediti osu rotacije. Započet ćemo s mjerenjem s materijalnom tačkom mase m, kutni impuls zapisan je skraćenicom L. Linearni impuls je p, a položaj čestice u odnosu na osu koja prolazi kroz određenu tačku O je r.

Ovako se izračunava na sljedeći način: L = rxp

Reaktor koji nastaje iz vektorskog proizvoda okomit je na ravninu koju tvore vektori koji sudjeluju. To znači da smjer smisao koji se može pronaći desnom rukom pravilo za unakrsni proizvod. Kutni moment se mjeri u jedinicama kg po kvadratnom metru / sekundi. Ovo se mjeri prema međunarodnom sistemu jedinica i nema posebna imena.

Ova definicija kutnog momenta ima najviše smisla za tijela koja se sastoje od mnogih čestica.

Iznos kutnog kretanja

Kutni moment momentne čestice koristimo za karakterizaciju stanja rotacije tačke ili tijela koje se može tretirati kao takvo. Zapamtite da se to događa kada su dimenzije tijela zanemarive u odnosu na putanju njegovog kretanja. U odnosu na vektore ugaonog momenta u odnosu na datu tačku i linearni impuls tačkaste čestice koji pomiče se kako je opseg kutni moment.

Za slučaj čestice koja se kreće u opsegu, kut je 90 stepeni. To je zato što je brzina kutnog momenta uvijek tangenta opsega i stoga okomita na radijus.

Kada govorimo o kutnom momentu, govorimo i o trenutku inercije. To nije ništa više od onoga što je opisano kada kruto tijelo ima inerciju vlastitog tijela protiv rotacije oko određene osi. Ovaj trenutak inercije ne ovisi samo o masi tijela, već i o udaljenosti od samog tijela do osi rotacije. To se može lakše razumjeti ako pomislimo da je za neke objekte lakše rotirati u odnosu na druge na istoj osi. To ovisi o formiranju i strukturi samog predmeta.

Za sisteme čestica trenutak inercije označava se slovom I i izračunava se prema sljedećoj formuli:

I = ∑r_i² Δm_i

Ovdje imamo da je njegova notorna vrijednost m mali dio mase, a r udaljenost koju tijelo ima u odnosu na osu rotacije. Tijelo će biti potpuno ispruženo i sastavljeno od brojnih čestica, stoga je njegov ukupni moment inercije zbroj svih proizvoda između mase i udaljenosti. Ovisi o geometriji koju imaju, zbrajanje se mijenja i ide od integralnog do diferencijalnog. Pojam momenta inercije usko je povezan s kutnim momentom objekta ili je potpuno proširen.

Kutni moment sistema čestica

Razmotrit ćemo sistem čestica koji se sastoji od različitih masa i koji se rotira prateći jedan opseg istovremeno u ravnini xy, od kojih svaka ima linearnu brzinu koja je povezana s kutnom brzinom. Na ovaj način se može izračunati ukupan sistem i daje se sljedećim zbrajanjem:

L = ω ∑r_i² Δm_i

Prošireno tijelo mogu se podijeliti na kriške svaka s različitim kutnim momentom. Ako se os simetrije predmetnog predmeta podudara sa z osi, nema problema. A to je zbog činjenice da postoje točke koje nisu u xy ravnini, pa se komponente koje je čine i koje su okomite na spomenutu os poništavaju.

Pogledajmo sada kada to varira. Obično, kada neto sila djeluje na tijelo ili česticu, zamah ovog konkretnog može se promijeniti. Kao posljedica toga bit će i kutni moment.

S druge strane, očuvanje se događa kada varira postojeći mjerač obrtnog momenta. Ako je taj obrtni moment jednak nuli, kutni moment se konstantno čuva. Ovaj rezultat i dalje vrijedi čak i u slučaju da tijelo nije potpuno kruto.

Primjeri momenta gibanja

Sve je ovo puno teorije i ne može se dobro razumjeti bez praktičnih primjera. Pogledajmo praktične primjere momenta gibanja. U prvom imamo umjetničko klizanje i druge sportove u kojima ima zaokreta. Kad se klizačica počne okretati, ona pruža ruke, a zatim nas skuplja uz naše tijelo kako bismo joj prekrižili noge. To se radi radi povećanja brzine okretanja. Kad god tijelo neprestano oscilira, ono se sabija. Zahvaljujući ovoj kontrakciji može povećati brzinu rotacije. To je zbog činjenice da činjenica da stežete ruke i noge takođe smanjuje trenutak inercije. Kako se kutni moment održava, ugaona brzina raste.

Drugi je primjer zašto mačke slijeću na noge. Iako nema početnu količinu pokreta, brine se da brzo izgovori i noge i rep kako bi promijenio svoju inerciju rotacije i mogao pasti s stopala. Dok manevriraju tim okretanjem, njihov kutni moment je nula, jer njihovo okretanje nije kontinuirano.

Nadam se da s ovim informacijama možete saznati više o tome.