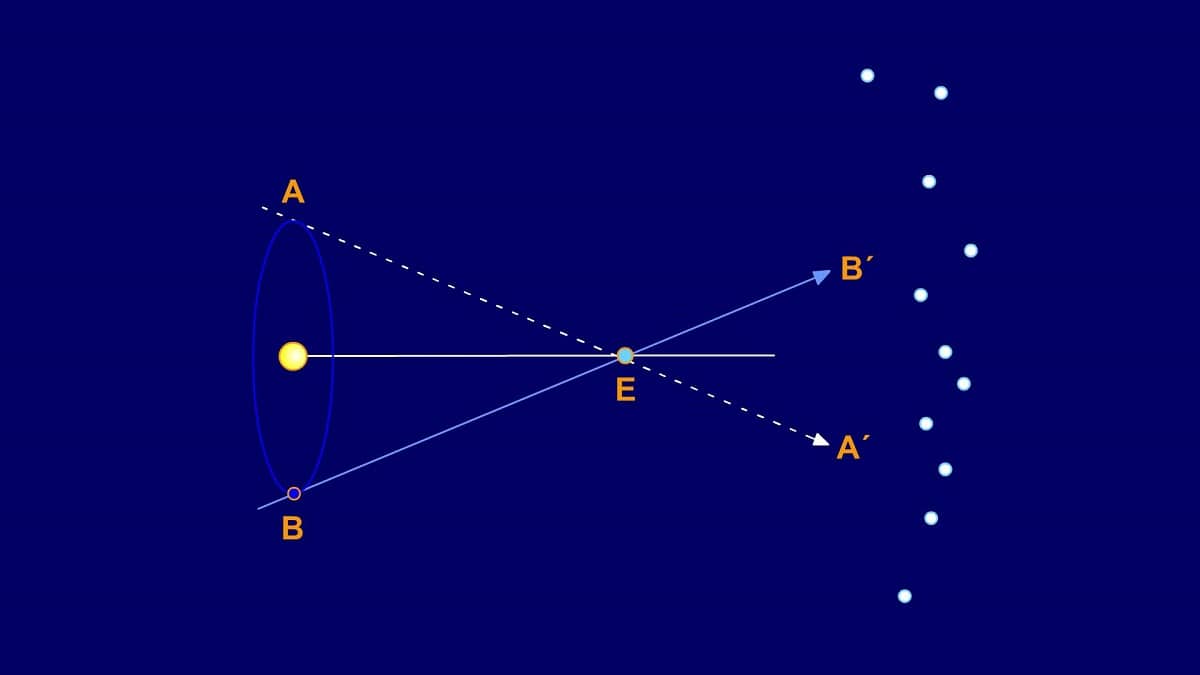
La 视差 是物体表观位置的角度偏差,取决于所选的视点。 这在天文学领域有一定的应用,既可以测量距离,也可以可视化天体。 很多人不知道什么是视差。
因此,在本文中,我们将告诉您视差是什么、它的特点是什么以及它的重要性。
什么是视差
视差涉及将手指放在眼前。 背景不应该是统一的。 在不移动头部或手指的情况下,先用一只眼睛看,然后再用另一只眼睛看,可以看出手指的位置相对于背景发生了变化。 如果我们将手指靠近眼睛,用一只眼睛再看一遍,然后再用另一只眼睛看, 背景上的两个手指位置覆盖了更大的部分。
这是因为双眼之间有几厘米的距离,所以连接手指和一只眼睛的假想线与连接手指和另一只眼睛的假想线形成一个角度。 如果我们将这两条假想的线延伸到底部,我们将有两个点对应于手指的两个不同位置。
我们将手指放在离眼睛越近的地方,角度就越大,表观位移就越大。 如果眼睛分开得更远,两条线形成的角度会增加更多,因此手指与背景的明显位移会更大。
天文学中的视差

这也适用于行星。 实际上, 月亮离我们很远,用眼睛看也看不出有什么不同. 但是,如果我们从相距数百公里的两个天文台以星空为背景观察月球,我们会注意到一些事情。 在第一个天文台,我们会看到月球的边缘与一颗特定恒星有一定距离,而在第二个天文台,相同的边缘与同一颗恒星的距离不同。
知道月球相对于星空背景的视位移以及两个天文台之间的距离,就可以借助三角学计算出这个距离。
这个实验非常有效,因为当改变观察者的位置时,月球相对于星空背景的明显位移非常大。 天文学家已将此偏移量标准化,以适应这样一种情况:一个观察者看到月亮在地平线上,而另一个观察者在它上方。 三角形的底边等于地球的半径,它与月球顶点的夹角就是“赤道水平视差”。 它的值为 57,04 弧分或 0,95 弧度。
事实上,这是一个相当大的位移,因为它相当于满月视直径的两倍。 这是一个可以足够精确地测量以获得到月球距离的良好值的量级。 这个距离是在视差的帮助下计算出来的,与通过地球在月食期间投下的阴影的旧方法获得的数字非常吻合。
不幸的是, 1600 年的条件不允许将天文台放置得足够远,再加上发现行星的距离很远,使得星空背景下的视位移太小而无法精确。
类型
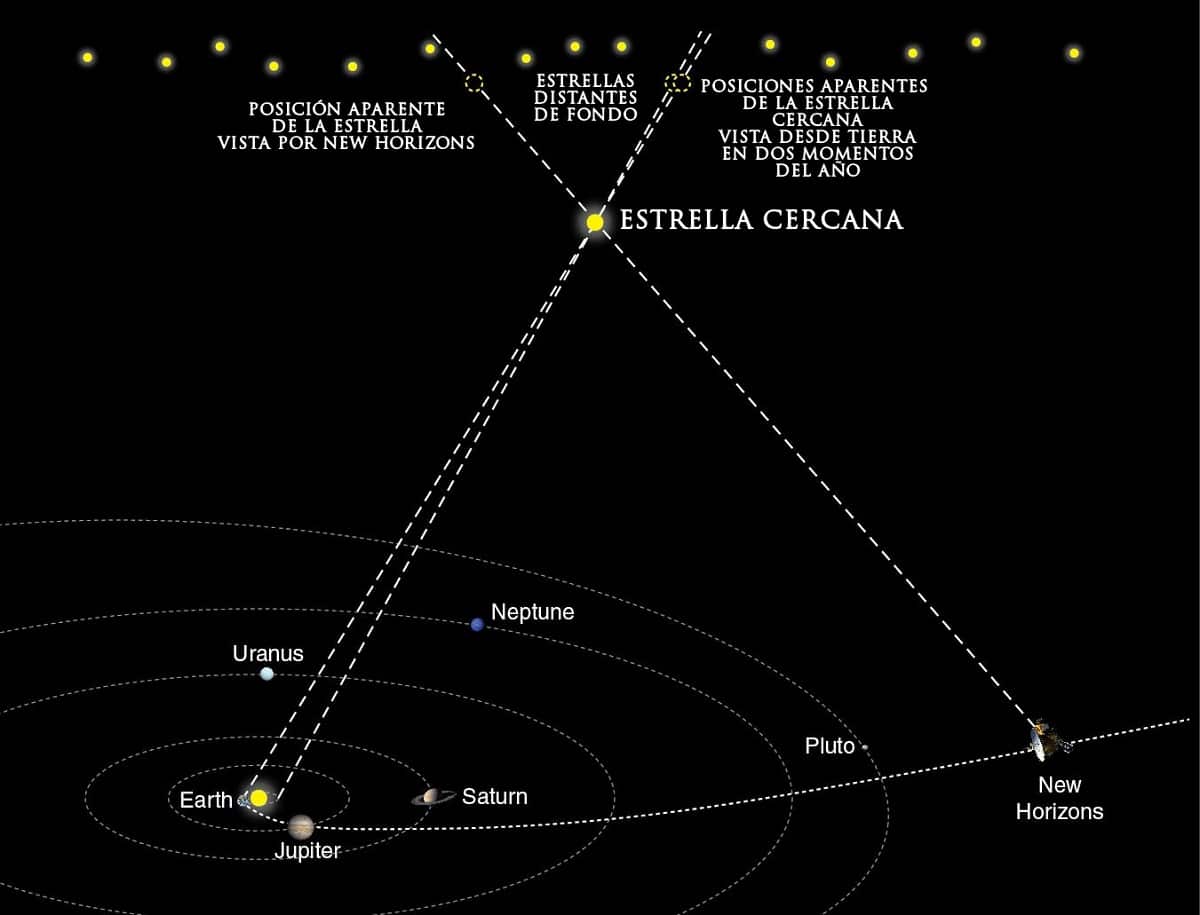
我们可以说有两种类型的视差:
- 地心视差: 当使用的半径是地面时。
- 年度质心或视差螺旋: 当使用的半径是地球绕太阳公转的轨道时。
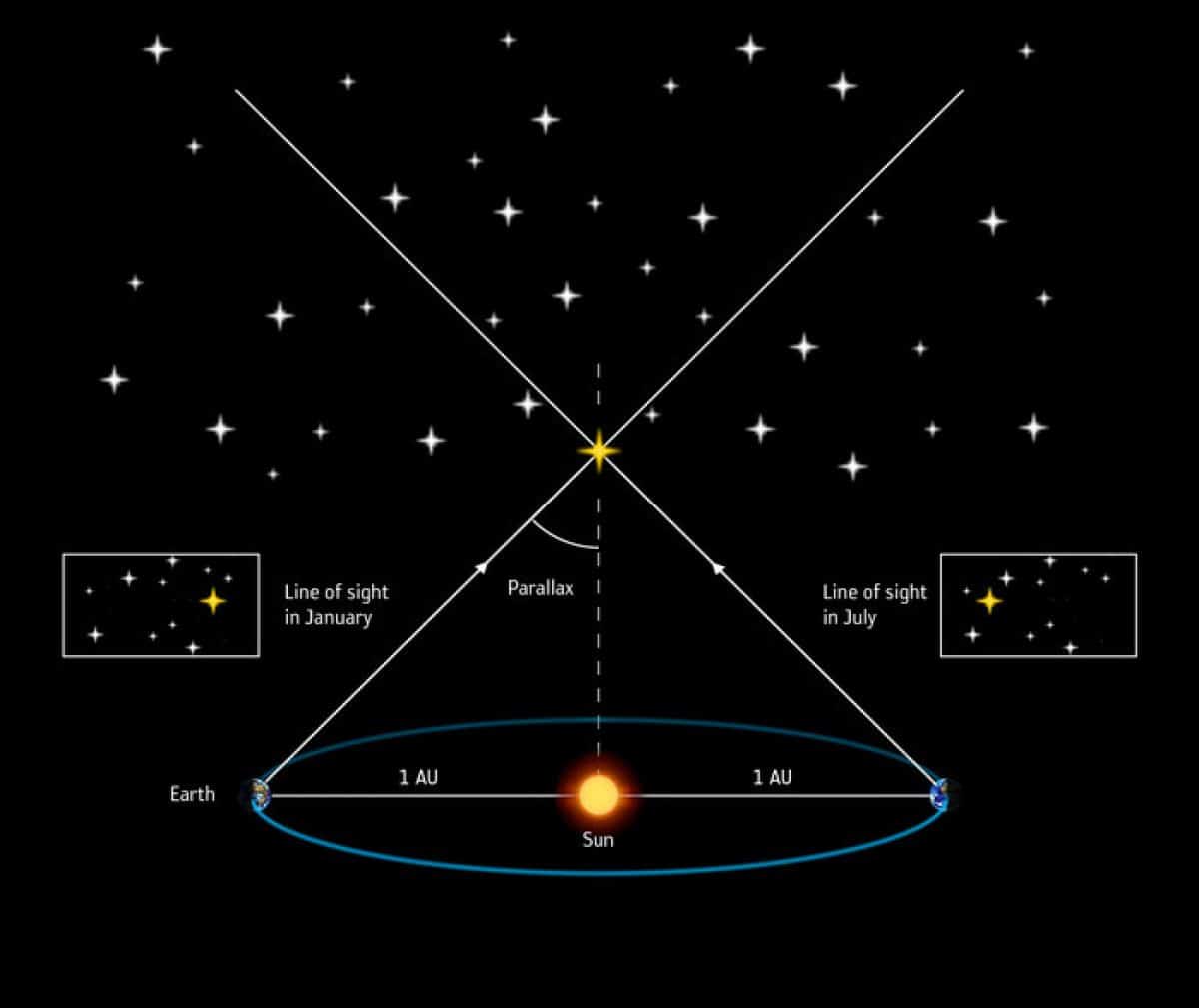
如果我们在一月和六月观察一颗恒星,地球将处于地球轨道的两个相对位置。 我们可以测量恒星表观位置的变化。 视差越大,那颗恒星就越近。 为此,秒差距被用作单位,它被定义为以弧秒为单位测量的三角视差的倒数。
视差调查
后来出现了意大利科学家伽利略·伽利莱发明或改进的望远镜。 望远镜可以轻松测量肉眼无法检测到的角距离。
视差最大的行星是最近的行星,即火星和金星。 金星在其最近经过时距离太阳如此之近,除非在凌日过程中在太阳圆盘的背景下可见,否则无法观察到它。 然后, 唯一测量视差的情况是火星。
行星视差的首次望远镜测量是在 1671 年进行的。两位观测者是率领科考队前往法属圭亚那卡宴的法国天文学家让·里歇尔和留在巴黎的意大利-法国天文学家乔瓦尼·卡西尼。 他们尽可能同时观察火星,并记下它相对于最近恒星的位置。 通过计算观测到的位置差,知道卡宴到巴黎的距离,就可以计算出测量时距火星的距离。
一旦完成,开普勒模型的比例将可用,使我们能够计算太阳系中的所有其他距离。 卡西尼号估计日地距离为 140 亿公里, 比实际数字少了9万公里,但第一次尝试的结果非常好。
后来,对行星视差进行了更精确的测量。 金星上的一些恰好在地球和太阳之间经过的地方,可以看作是太阳圆盘上的一个小黑圈。 这些凌日发生在1761年和1769年。如果从两个不同的天文台可以验证金星与太阳盘接触的时刻和它与太阳盘分离的时刻,即, 从一个天文台到另一个天文台,过境的持续时间不同。 知道了这些变化和两个天文台之间的距离,就可以计算出金星的视差。 使用这些数据,您可以计算到金星的距离,然后再计算到太阳的距离。
我希望通过这些信息,您可以更多地了解什么是视差及其特性。