
Një fraktal është një objekt gjeometrik që mund të ndahet në pjesë, secila e ngjashme me objektin origjinal. Fraktalet kanë detaje të pafundme dhe shpesh janë të ngjashëm dhe të shkallëzuar. Ne shume raste, fraktale ato mund të gjenerohen nga modele të përsëritura, procese rekursive ose përsëritëse.
Në këtë artikull do t'ju tregojmë gjithçka që duhet të dini për fraktalet, karakteristikat dhe rëndësinë e tyre.
Vetitë e fraktaleve

Vetitë kryesore që karakterizojnë fraktalet janë vetëngjashmëria, kompleksiteti i pafund dhe dimensionaliteti.
ngjashmëria e vetvetes
Vetëngjashmëria është kur një pjesë e një figure ose skicë mund të shihet si një kopje e së tërës, në një shkallë më të vogël.
kompleksiteti i pafund
I referohet faktit që procesi i formimit të grafikut është rekurziv. Kjo do të thotë se kur një procedurë ekzekutohet, vetë procedura e ekzekutuar më parë rezulton të jetë një nënprocedurë në procedurën e saj.
Vlen të theksohet se në rastin e ndërtimit iterativ të një fraktali të përcaktuar matematikisht, programi që do të ekzekutohet është i pafund, gjë që rezulton në një strukturë pafundësisht komplekse.
përmasat
Ndryshe nga gjeometria Euklidiane, dimensionet e fraktaleve nuk janë domosdoshmërisht vlera të plota. Në këtë degë të matematikës, pikat kanë dimension zero, vijat kanë një dimension, sipërfaqet kanë dy dimensione dhe vëllimet kanë tre dimensione. Në rastin e dimensionit fraktal, kjo është një sasi fraksionale që përfaqëson se sa mirë një strukturë zë hapësirën që e përmban atë.
shembuj të fraktaleve

Fraktalet e para të studiuara ishin grupi Cantor, flok dëbore Koch dhe trekëndëshi Sierpinski. Fraktalet mund të merren gjeometrikisht ose stokastikisht përmes proceseve rekursive dhe mund të marrin karakteristikat e llojeve të ndryshme të formave që gjenden në natyrë.
Fraktalet ekzistojnë kudo. Ka shumë objekte natyrore që konsiderohen fraktale natyrore për shkak të sjelljes ose strukturës së tyre, por këto janë lloje të fundme fraktalesh, që i dallojnë ato nga fraktale të tipit matematik të krijuar nga ndërveprimet rekursive. Shembuj të tillë janë retë dhe pemët.
tipare kryesore
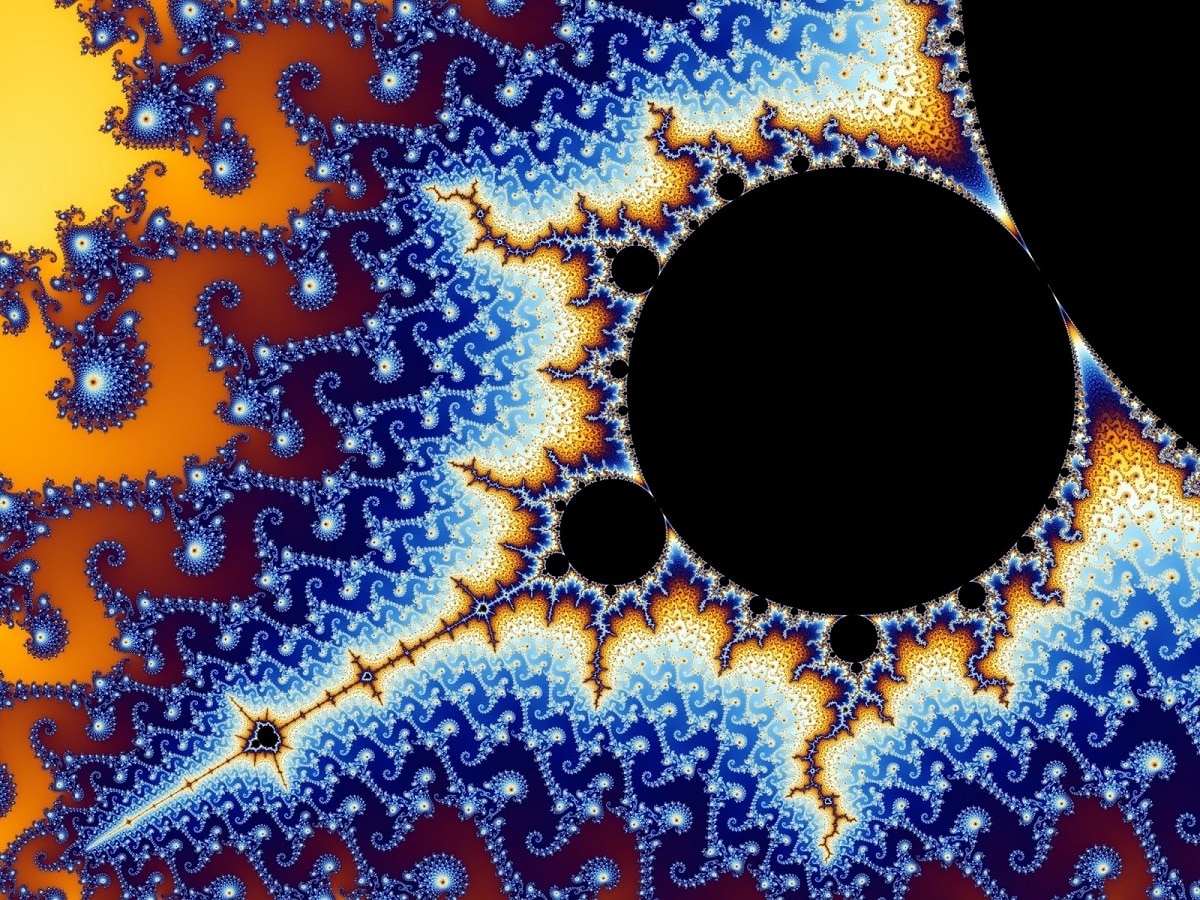
Fjala "fractal" vjen nga latinishtja fractus, që do të thotë "i copëtuar", "i thyer", ose thjesht "i thyer" ose "i thyer" dhe i përshtatet mirë objekteve me dimensione të pjesshme. Termi u krijua nga Benoît Mandelbrot në 1977 dhe u shfaq në librin e tij Gjeometria Fractal e Natyrës. Studimi i objekteve fraktal shpesh quhet gjeometri fraktal.
Një fraktal është një grup matematikor që mund të gëzojë vetëngjashmëri në çdo shkallë, dhe dimensionet e tij nuk janë numra të plotë, ose nëse do të ishin, nuk do të ishin numra të plotë të zakonshëm. Fakti që është i ngjashëm do të thotë që objekti fraktal nuk varet nga vetë vëzhguesi, domethënë nëse marrim një lloj fraktali, mund të verifikojmë që kur zmadhojmë dyfish, vizatimi është i njëjtë me të parën. Nëse zmadhojmë me një faktor 1000, verifikojmë të njëjtat veti, kështu që nëse rritim n, grafiku është i njëjtë, pra pjesa është e ngjashme me të tërën.
Një koleksion ose objekt thuhet se është fraktal kur bëhet në mënyrë arbitrare i madh ndërsa shkalla e instrumentit matës zvogëlohet. Ka shumë objekte të zakonshme që konsiderohen të natyrshme për shkak të strukturës ose sjelljes së tyre.Edhe nëse nuk i njohim. Retë, malet, vijat bregdetare, pemët dhe lumenjtë janë të gjitha fraktale natyrore, megjithëse të fundme dhe për këtë arsye jo ideale, ndryshe nga fraktalet matematikore që gëzojnë pafundësi dhe janë ideale.
Fraktalet dhe shkenca
Arti fraktal është i lidhur ngushtë me matematikën, veçanërisht me gjeometrinë, pasi, siç sugjeron emri i tij, ai përdor konceptin e fraktaleve. Fraktalet bazohen në përsëritjen e vazhdueshme të një modeli gjeometrik të vetë-korreluar, domethënë, pjesa është e barabartë me të gjithë.
Kur ndërtoni trekëndëshin e Sierpinskit, nga një trekëndësh barabrinjës, merrni mesin e tij, formoni një trekëndësh të ri barabrinjës dhe eliminoni atë qendror. Pastaj bëni të njëjtën gjë me çdo trekëndësh të mbetur, e kështu me radhë, pra konsiderohet fraktal. Benoit Mandelbrot, i cili zbuloi format matematikore të njohura si fraktale, ka vdekur nga kanceri në moshën 85-vjeçare. Mandelbrot, një qytetar francez dhe amerikan, zhvilloi fraktale si një metodë matematikore për të kuptuar kompleksitetin e pafund të natyrës.
Për të trajtuar klasifikimin nga i përgjithshëm në të veçantë, ne mund t'i ndajmë ato në dy kategori të gjera: fraktale përcaktuese (të cilat nga ana tjetër mund të jenë algjebrike ose gjeometrike) dhe fraktale jo-përcaktuese (të njohura edhe si fraktale stokastike).
Fraktalet lineare janë ato që ndërtohen pasi shkallët ndryshojnë, domethënë janë identike në të gjitha shkallët. Fraktale jolineare, nga ana tjetër, rezulton nga shtrembërime komplekse, ose siç sugjeron emri, për të përdorur një term në matematikën kaotike, shtrembërime jolineare.
Jeta e perditshme
Shumica e objekteve thjesht matematikore dhe natyrore janë jolineare. Në matematikë, vetëngjashmëria, e quajtur ndonjëherë vetëngjashmëri, është një veti e një objekti (i quajtur objekt i vetëngjashëm) në të cilin e tëra është saktësisht ose afërsisht e ngjashme me të njëjtën pjesë, për shembull kur e tëra ka të njëjtën një ose më shumë në formën e pjesëve të tij.
Një fraktal karakterizohet nga një perimetër që tenton në pafundësi si shtoni detaje gjithnjë e më të vogla me përsëritje të njëpasnjëshme. Megjithatë, kjo kurbë nuk mbivendos asnjë kufizim kohor të rrethit që rrethon trekëndëshin fillestar. Retë, malet, sistemet e qarkullimit të gjakut, vijat bregdetare ose floket e borës janë të gjitha fraktale natyrore. Ky përfaqësim është i përafërt sepse vetitë e objekteve ideale, të tilla si detajet e pafundme, janë të kufizuara në natyrë.
Gjeometria fraktale përpiqet të modelojë dhe përshkruajë shumë dukuri natyrore dhe eksperimente shkencore, dhe në vetëm pak vite është bërë një mjet multidisiplinar i përdorur nga shkencëtarë, mjekë, artistë, sociologë, ekonomistë, meteorologë, muzikantë, shkencëtarë kompjuterikë, Etj
Shpresoj që me këtë informacion të mund të mësoni më shumë rreth fraktaleve dhe karakteristikave të tyre.