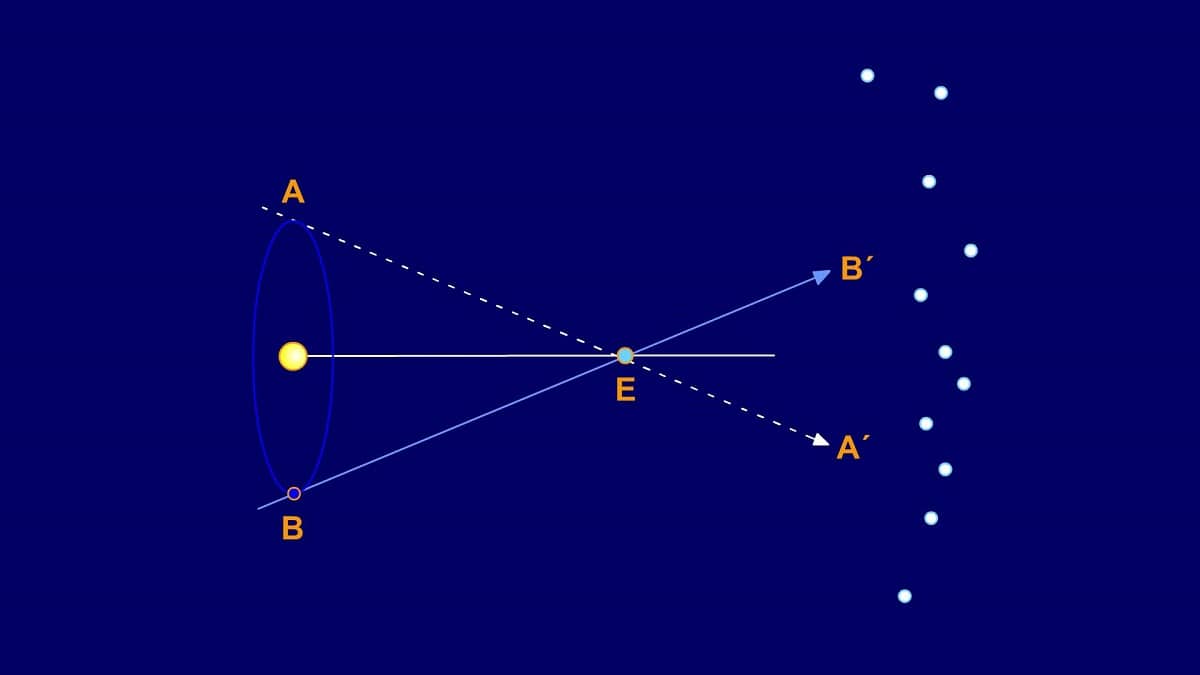
La लंब निवडलेल्या दृष्टिकोनावर अवलंबून, ऑब्जेक्टच्या स्पष्ट स्थितीचे कोनीय विचलन आहे. अंतर मोजण्यासाठी आणि खगोलीय वस्तूंची कल्पना करण्यासाठी याला खगोलशास्त्राच्या जगात काही विशिष्ट अनुप्रयोग आहेत. पॅरलॅक्स म्हणजे काय हे अनेकांना माहीत नाही.
म्हणूनच, या लेखात आम्ही तुम्हाला पॅरलॅक्स म्हणजे काय, त्याची वैशिष्ट्ये आणि त्याचे महत्त्व सांगणार आहोत.
पॅरलॅक्स म्हणजे काय
पॅरलॅक्समध्ये तुमच्या डोळ्यांसमोर बोटे ठेवणे समाविष्ट आहे. पार्श्वभूमी एकसमान नसावी. डोके किंवा बोट न हलवता प्रथम एका डोळ्याने आणि नंतर दुसऱ्या डोळ्याने पाहिल्यास, पार्श्वभूमीच्या संदर्भात बोटाची स्थिती बदलत असल्याचे दिसून येते. जर आपण आपले बोट डोळ्याच्या जवळ आणले आणि पुन्हा एका डोळ्याने आणि नंतर दुसऱ्या डोळ्याने पाहिले, पार्श्वभूमीवरील दोन बोटांची स्थिती एक मोठा भाग व्यापते.
कारण डोळ्यांमध्ये काही सेंटीमीटर असतात, त्यामुळे बोटांना एका डोळ्याला जोडणारी काल्पनिक रेषा बोटांना दुसऱ्या डोळ्याशी जोडणारी काल्पनिक रेषा एक कोन बनवते. जर आपण या दोन काल्पनिक रेषा तळाशी वाढवल्या तर आपल्याकडे बोटांच्या दोन भिन्न स्थानांशी संबंधित दोन बिंदू असतील.
आपण डोळ्याच्या बोटाला जितके जवळ ठेवतो तितका कोन मोठा आणि स्पष्ट विस्थापन जास्त. जर डोळे आणखी वेगळे असतील तर, दोन ओळींनी तयार केलेला कोन अधिक वाढेल, त्यामुळे पार्श्वभूमीतून बोटाचे स्पष्ट विस्थापन मोठे होईल.
खगोलशास्त्रातील समांतर

हे ग्रहांनाही लागू होते. खरं तर, चंद्र इतका दूर आहे की आपण त्याला डोळ्यांनी पाहिल्यावर काही फरक सांगू शकत नाही. परंतु आपण शेकडो किलोमीटर अंतरावर असलेल्या दोन वेधशाळांमधून तारांकित आकाशाच्या पार्श्वभूमीवर चंद्राकडे पाहिले तर आपल्याला काही गोष्टी लक्षात येतात. पहिल्या वेधशाळेतून आपल्याला एका विशिष्ट तार्यापासून ठराविक अंतरावर चंद्राची धार दिसेल, तर दुसऱ्या वेधशाळेत तीच धार त्याच ताऱ्यापासून वेगळ्या अंतरावर असेल.
तारकीय पार्श्वभूमी आणि दोन वेधशाळांमधील अंतर यांच्या संदर्भात चंद्राचे स्पष्ट विस्थापन जाणून घेतल्यास, हे अंतर त्रिकोणमितीच्या मदतीने मोजले जाऊ शकते.
हा प्रयोग उत्तम प्रकारे कार्य करतो कारण निरीक्षकाची स्थिती बदलताना तारामय आकाशाच्या पार्श्वभूमीच्या संदर्भात चंद्राचे स्पष्ट विस्थापन खूप मोठे असते. खगोलशास्त्रज्ञांनी ही ऑफसेट सामान्य केली आहे ज्यामध्ये एक निरीक्षक चंद्र क्षितिजावर पाहतो तर दुसरा त्याच्या वर असतो. त्रिकोणाचा पाया पृथ्वीच्या त्रिज्याएवढा आहे आणि तो चंद्राच्या शिरोबिंदूशी जो कोन बनवतो तो "विषुववृत्तावरील क्षैतिज समांतर" आहे. त्याचे मूल्य 57,04 मिनिटे चाप किंवा 0,95 रेडियन आहे.
खरं तर, लक्षणीय विस्थापन, कारण ते पौर्णिमेच्या स्पष्ट व्यासाच्या दुप्पट आहे. हे एक मोठेपणा आहे जे चंद्राच्या अंतरासाठी चांगले मूल्य मिळविण्यासाठी पुरेशा अचूकतेने मोजले जाऊ शकते. पॅरॅलॅक्सच्या साहाय्याने मोजले जाणारे हे अंतर, चंद्रग्रहणाच्या वेळी पृथ्वीने टाकलेल्या सावल्यांच्या जुन्या पद्धतीद्वारे मिळवलेल्या आकड्यांशी अगदी जुळते.
दुर्दैवाने, 1600 मधील परिस्थितीने वेधशाळा पुरेशी ठेवू दिली नाही, ज्याने ग्रहांचा शोध लावलेल्या मोठ्या अंतरांसह एकत्रितपणे, तारामय आकाशाच्या पार्श्वभूमीवर स्पष्ट विस्थापन अगदी लहान केले.
प्रकार
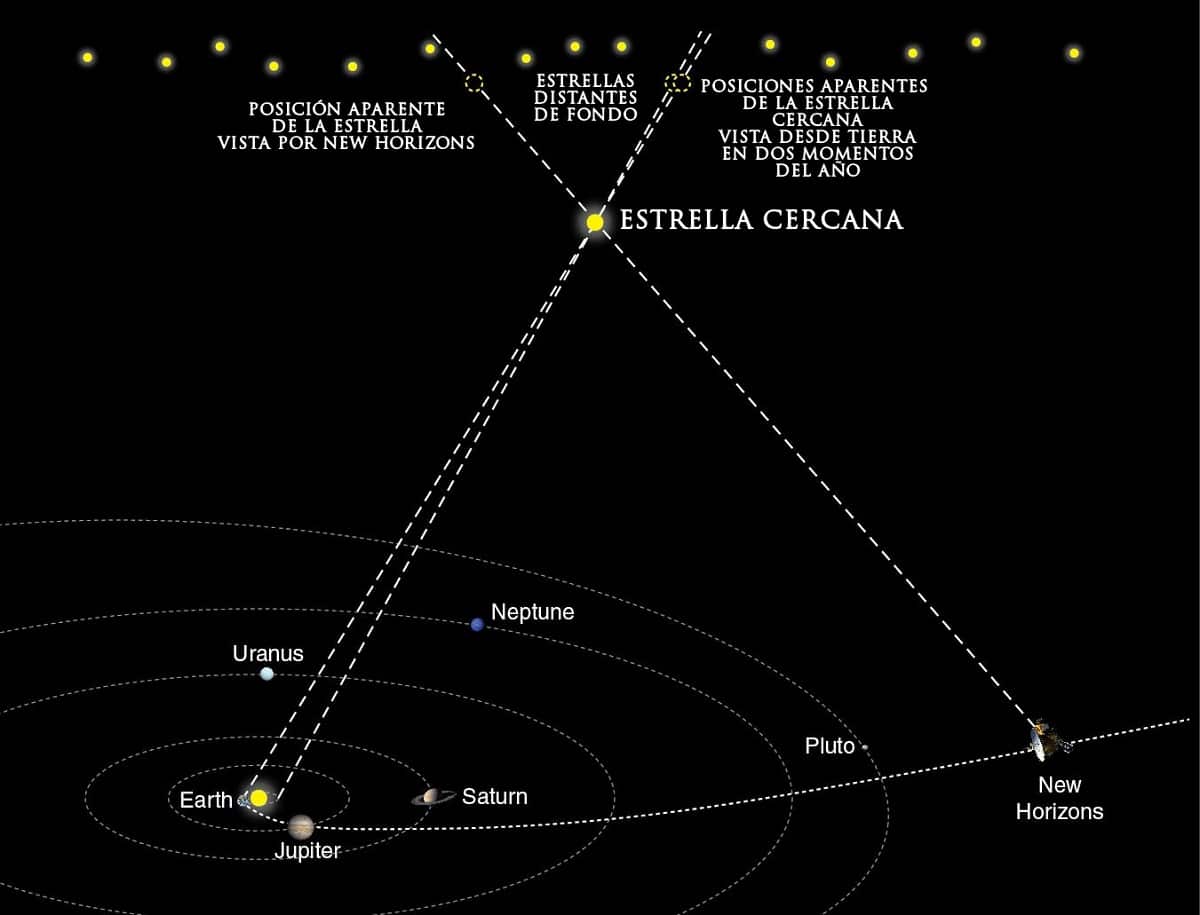
आपण असे म्हणू शकतो की पॅरलॅक्सचे दोन प्रकार आहेत:
- भूकेंद्रित लंबन: जेव्हा त्रिज्या वापरली जाते तेव्हा जमीन असते.
- वार्षिक सेंट्रोइड किंवा पॅरलॅक्स सर्पिल: जेव्हा त्रिज्या वापरली जाते तेव्हा पृथ्वीची सूर्याभोवतीची कक्षा असते.
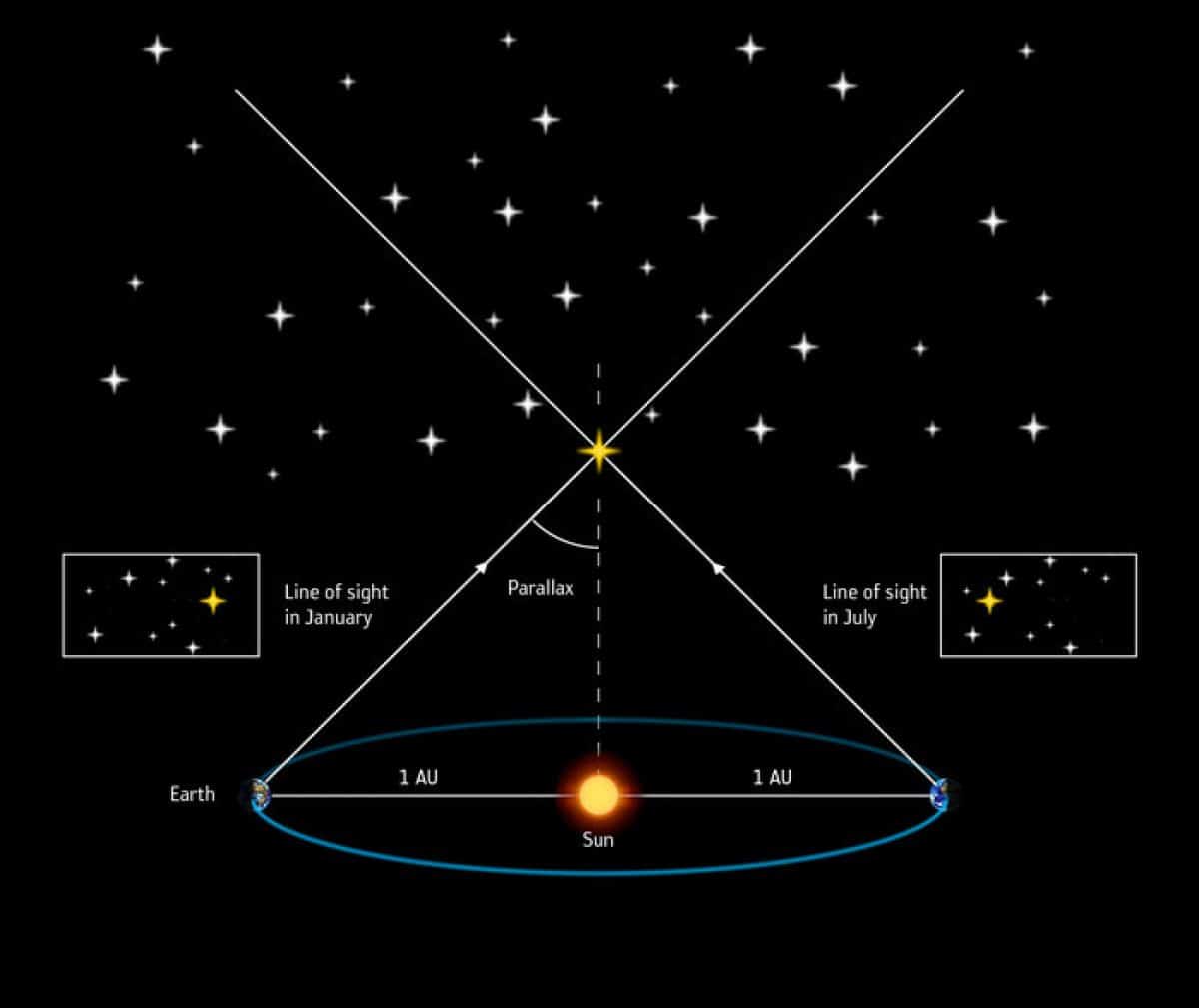
जर आपण जानेवारी आणि जूनमध्ये तारेचे निरीक्षण केले तर पृथ्वी पृथ्वीच्या कक्षेत दोन सापेक्ष स्थितीत असेल. आपण ताऱ्याच्या स्पष्ट स्थितीतील बदल मोजू शकतो. पॅरलॅक्स जितका मोठा असेल तितका तो तारा जवळ असेल. यासाठी, पार्सेक हे युनिट म्हणून वापरले जाते, ज्याची व्याख्या कमानीच्या सेकंदात मोजलेल्या त्रिकोणी पॅरलॅक्सच्या परस्पर म्हणून केली जाते.
पॅरालॅक्स तपासणी
नंतर इटालियन शास्त्रज्ञ गॅलिलिओ गॅलीली यांनी शोधलेल्या किंवा सुधारित दुर्बिणी आल्या. दुर्बिणी सहजपणे कोनीय अंतर मोजू शकतात जे उघड्या डोळ्यांनी शोधले जाऊ शकत नाहीत.
सर्वात मोठे समांतर असलेले ग्रह सर्वात जवळचे ग्रह आहेत, म्हणजे मंगळ आणि शुक्र. शुक्र त्याच्या सर्वात जवळच्या पास दरम्यान सूर्याच्या इतका जवळ असतो की त्याच्या संक्रमणादरम्यान सौर डिस्कच्या पार्श्वभूमीवर दृश्यमान असल्याशिवाय त्याचे निरीक्षण करता येत नाही. मग, पॅरॅलॅक्स मोजले जाणारे एकमेव प्रकरण मंगळ आहे.
1671 मध्ये ग्रहांच्या पॅरालॅक्सचे पहिले दुर्बिणीद्वारे मोजमाप केले गेले. दोन निरीक्षक फ्रेंच खगोलशास्त्रज्ञ जीन रिचेल होते, ज्यांनी केयेन, फ्रेंच गयाना येथे वैज्ञानिक मोहिमेचे नेतृत्व केले आणि इटालियन-फ्रेंच खगोलशास्त्रज्ञ जियोव्हानी कॅसिनी, जे पॅरिसमध्ये राहिले. त्यांनी शक्य तितक्याच वेळी मंगळाचे निरीक्षण केले आणि जवळच्या ताऱ्याच्या तुलनेत त्याची स्थिती लक्षात घेतली. निरीक्षण केलेल्या स्थितीतील फरकाची गणना करून, केयेनपासून पॅरिसपर्यंतचे अंतर जाणून घेऊन, मापनाच्या वेळी मंगळापासूनचे अंतर मोजले जाते.
पूर्ण झाल्यावर, केप्लर मॉडेलचे स्केल उपलब्ध होईल, ज्यामुळे आम्हाला सौर यंत्रणेतील इतर सर्व अंतरांची गणना करता येईल. कॅसिनीने सूर्य-पृथ्वीतील अंतर 140 दशलक्ष किलोमीटर असल्याचे सांगितले. वास्तविक आकृतीपेक्षा 9 दशलक्ष किलोमीटर कमी, परंतु पहिल्या प्रयत्नाचे परिणाम खूप चांगले होते.
नंतर, ग्रहांच्या पॅरालॅक्सचे अधिक अचूक मापन केले गेले. शुक्रावरील काही, जिथे तो पृथ्वी आणि सूर्य यांच्यामधून जातो, ते सौर डिस्कवर एक लहान गडद वर्तुळ म्हणून दिसू शकतात. हे संक्रमण 1761 आणि 1769 मध्ये झाले. जर दोन वेगवेगळ्या वेधशाळांमधून हे सत्यापित केले जाऊ शकते की शुक्राचा सौर डिस्कशी संपर्काचा क्षण आणि सौर डिस्कपासून विभक्त होण्याचा क्षण, म्हणजे, संक्रमणाचा कालावधी एका वेधशाळेपासून दुसऱ्या वेधशाळेत वेगळा असतो. हे बदल आणि दोन वेधशाळांमधील अंतर जाणून घेतल्यास शुक्राचा समांतर मोजता येतो. या डेटाद्वारे तुम्ही शुक्र आणि नंतर सूर्यापर्यंतचे अंतर मोजू शकता.
मला आशा आहे की या माहितीसह आपण पॅरलॅक्स म्हणजे काय आणि त्याची वैशिष्ट्ये याबद्दल अधिक जाणून घेऊ शकता.