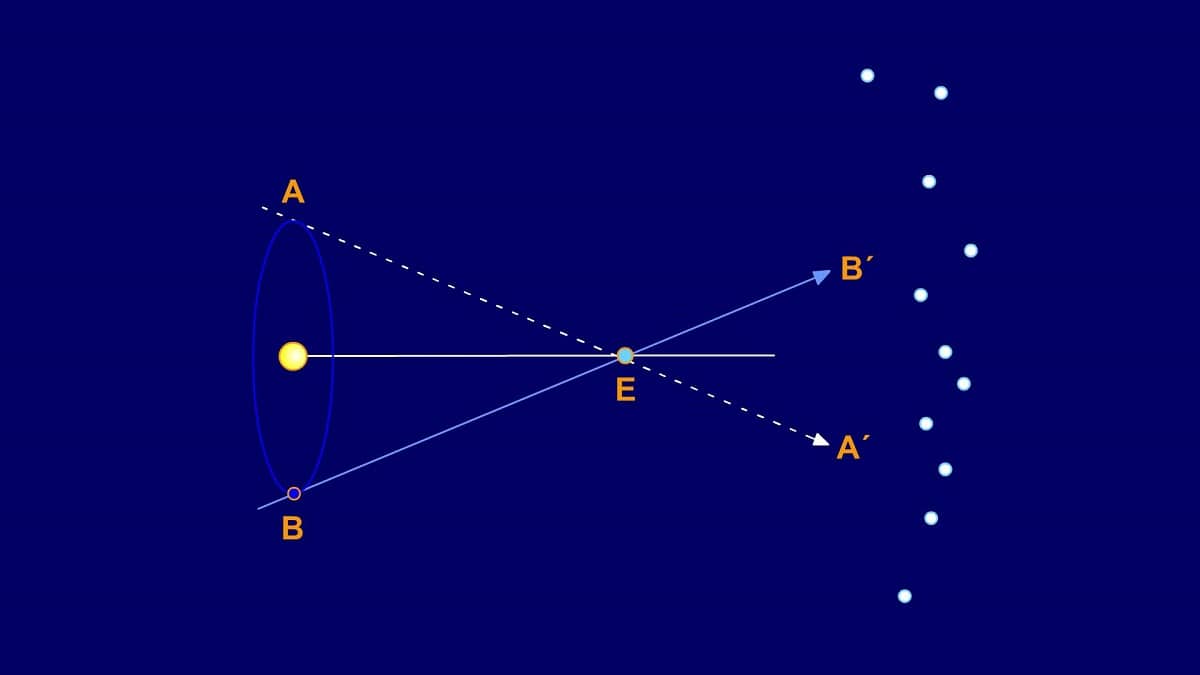
La લંબન પસંદ કરેલા દૃષ્ટિકોણ પર આધાર રાખીને ઑબ્જેક્ટની દેખીતી સ્થિતિનું કોણીય વિચલન છે. અંતરને માપવા અને અવકાશી પદાર્થોની કલ્પના કરવા માટે આ ખગોળશાસ્ત્રની દુનિયામાં ચોક્કસ એપ્લિકેશન ધરાવે છે. ઘણા લોકો જાણતા નથી કે લંબન શું છે.
તેથી, આ લેખમાં અમે તમને લંબન શું છે, તેની વિશેષતાઓ શું છે અને તેનું મહત્વ જણાવવા જઈ રહ્યા છીએ.
લંબન શું છે
લંબન તમારી આંખો સામે તમારી આંગળીઓ મૂકવાનો સમાવેશ કરે છે. પૃષ્ઠભૂમિ એકસરખી ન હોવી જોઈએ. માથું કે આંગળી ખસેડ્યા વિના પહેલા એક આંખથી અને પછી બીજી આંખથી જોતા, તે જોઈ શકાય છે કે પૃષ્ઠભૂમિના સંદર્ભમાં આંગળીની સ્થિતિ બદલાય છે. જો આપણે આપણી આંગળી આંખની નજીક લાવીએ અને ફરી એક આંખથી અને પછી બીજી આંખથી જોઈએ, પૃષ્ઠભૂમિ પરની બે આંગળીઓની સ્થિતિ મોટા ભાગને આવરી લે છે.
આ એટલા માટે છે કારણ કે આંખો વચ્ચે થોડા સેન્ટિમીટર છે, તેથી આંગળીઓને એક આંખ સાથે જોડતી કાલ્પનિક રેખા આંગળીઓને બીજી આંખ સાથે જોડતી કાલ્પનિક રેખા સાથે કોણ બનાવે છે. જો આપણે આ બે કાલ્પનિક રેખાઓને તળિયે લંબાવીશું, તો આપણી પાસે આંગળીઓની બે જુદી જુદી સ્થિતિને અનુરૂપ બે બિંદુઓ હશે.
આંખની નજીક આપણે આંગળીને જેટલી નજીક રાખીએ છીએ, તેટલો મોટો કોણ અને વધુ સ્પષ્ટ વિસ્થાપન. જો આંખો વધુ અલગ હશે, તો બે રેખાઓ દ્વારા રચાયેલ કોણ વધુ વધશે, તેથી પૃષ્ઠભૂમિમાંથી આંગળીનું સ્પષ્ટ વિસ્થાપન વધારે હશે.
ખગોળશાસ્ત્રમાં લંબન

આ ગ્રહોને પણ લાગુ પડે છે. હકિકતમાં, ચંદ્ર એટલો દૂર છે કે જ્યારે આપણે તેને આપણી આંખોથી જોઈએ છીએ ત્યારે આપણે કોઈ તફાવત કહી શકતા નથી. પરંતુ જો આપણે સેંકડો કિલોમીટરના અંતરે બે વેધશાળાઓમાંથી તારાવાળા આકાશની પૃષ્ઠભૂમિ સામે ચંદ્રને જોઈએ છીએ, તો આપણે કેટલીક બાબતો નોંધીએ છીએ. પ્રથમ વેધશાળામાંથી આપણે ચોક્કસ તારાથી ચોક્કસ અંતરે ચંદ્રની ધાર જોઈશું, જ્યારે બીજી વેધશાળામાં તે જ ધાર એક જ તારાથી અલગ અંતરે હશે.
તારાઓની પૃષ્ઠભૂમિ અને બે વેધશાળાઓ વચ્ચેના અંતરના સંદર્ભમાં ચંદ્રના દેખીતા વિસ્થાપનને જાણતા, ત્રિકોણમિતિની મદદથી આ અંતરની ગણતરી કરી શકાય છે.
આ પ્રયોગ સંપૂર્ણ રીતે કામ કરે છે કારણ કે જ્યારે નિરીક્ષકની સ્થિતિ બદલાતી હોય ત્યારે તારાઓવાળા આકાશની પૃષ્ઠભૂમિના સંદર્ભમાં ચંદ્રનું દેખીતું વિસ્થાપન ખૂબ મોટું હોય છે. ખગોળશાસ્ત્રીઓએ પરિસ્થિતિને સમાવવા માટે આ ઑફસેટને સામાન્ય બનાવ્યું છે જેમાં એક નિરીક્ષક ક્ષિતિજ પર ચંદ્ર જુએ છે જ્યારે બીજો તેની ઉપર છે. ત્રિકોણનો આધાર પૃથ્વીની ત્રિજ્યા જેટલો છે અને તે ચંદ્રના શિરોબિંદુ સાથે જે કોણ બનાવે છે તે "વિષુવવૃત્ત પર આડી લંબન" છે. તેનું મૂલ્ય 57,04 મિનિટ આર્ક અથવા 0,95 રેડિયન છે.
હકીકતમાં, નોંધપાત્ર વિસ્થાપન, કારણ કે તે પૂર્ણ ચંદ્રના દેખીતા વ્યાસના બમણા સમાન છે. આ એક તીવ્રતા છે જે ચંદ્રના અંતર માટે સારી કિંમત મેળવવા માટે પૂરતી ચોકસાઇ સાથે માપી શકાય છે. આ અંતર, લંબનની મદદથી ગણવામાં આવે છે, ચંદ્રગ્રહણ દરમિયાન પૃથ્વી દ્વારા પડછાયાઓની જૂની પદ્ધતિ દ્વારા મેળવેલા આંકડાઓ સાથે ખૂબ જ સારી રીતે સંમત થાય છે.
કમનસીબે 1600ની પરિસ્થિતિઓએ વેધશાળાને ખૂબ દૂર રાખવાની મંજૂરી આપી ન હતી, જે, ગ્રહોની શોધ કરવામાં આવેલા મહાન અંતર સાથે મળીને, તારાઓવાળા આકાશની પૃષ્ઠભૂમિ સામે દેખીતા વિસ્થાપનને ચોક્કસ હોવા માટે ખૂબ નાનું બનાવ્યું.
પ્રકારો
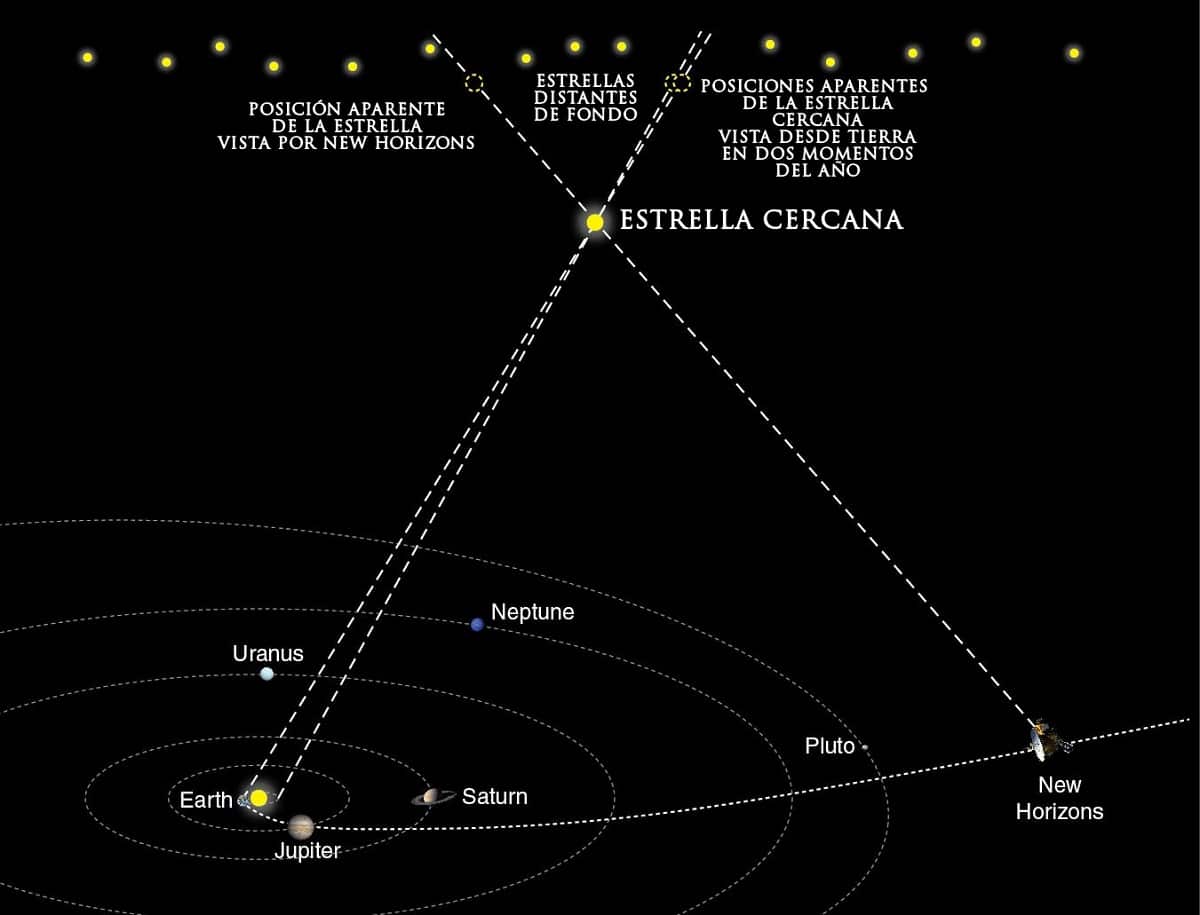
આપણે કહી શકીએ કે લંબન બે પ્રકારના હોય છે:
- ભૂકેન્દ્રીય લંબન: જ્યારે વપરાયેલ ત્રિજ્યા જમીન છે.
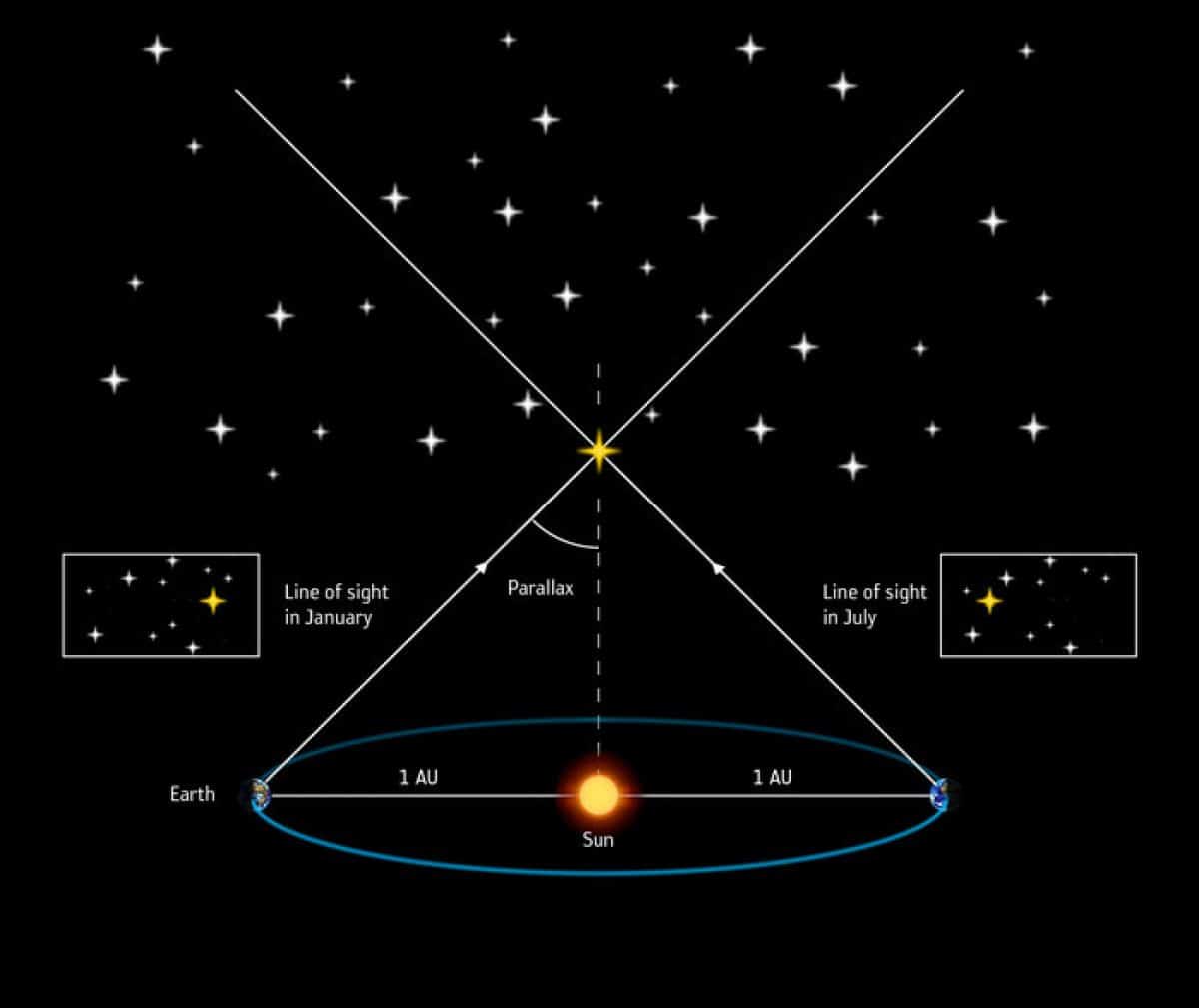
- સર્પાકાર સેન્ટ્રોઇડ અથવા વાર્ષિક લંબન: જ્યારે વપરાયેલ ત્રિજ્યા એ સૂર્યની આસપાસ પૃથ્વીની ભ્રમણકક્ષા છે.
જો આપણે જાન્યુઆરી અને જૂનમાં તારાનું અવલોકન કરીએ, તો પૃથ્વી પૃથ્વીની ભ્રમણકક્ષામાં બે સંબંધિત સ્થિતિમાં હશે. અમે તારાની દેખીતી સ્થિતિમાં ફેરફારોને માપી શકીએ છીએ. લંબન જેટલું મોટું છે, તે તારો નજીક છે. આ માટે, પાર્સેકનો ઉપયોગ એકમ તરીકે થાય છે, જેને ચાપની સેકન્ડોમાં માપવામાં આવતા ત્રિકોણાકાર લંબનના પરસ્પર તરીકે વ્યાખ્યાયિત કરવામાં આવે છે.
લંબન તપાસ
પાછળથી ઇટાલિયન વૈજ્ઞાનિક ગેલિલિયો ગેલિલી દ્વારા ટેલિસ્કોપની શોધ કરવામાં આવી અથવા તેમાં ફેરફાર કરવામાં આવ્યો. ટેલિસ્કોપ સરળતાથી કોણીય અંતર માપી શકે છે જે નરી આંખે શોધી શકાતા નથી.
સૌથી મોટા લંબનવાળા ગ્રહો સૌથી નજીકના ગ્રહો છે, એટલે કે મંગળ અને શુક્ર. શુક્ર તેના સૌથી નજીકના પાસ દરમિયાન સૂર્યની એટલો નજીક છે કે જ્યારે તે તેના સંક્રમણ દરમિયાન સૌર ડિસ્કની પૃષ્ઠભૂમિ સામે દૃશ્યમાન હોય તે સિવાય તેનું અવલોકન કરી શકાતું નથી. પછી, એકમાત્ર કેસ જ્યાં લંબન માપવામાં આવે છે તે મંગળ છે.
ગ્રહોના લંબનનું પ્રથમ ટેલિસ્કોપિક માપન 1671 માં કરવામાં આવ્યું હતું. બે નિરીક્ષકો ફ્રેન્ચ ખગોળશાસ્ત્રી જીન રિશેલ હતા, જેમણે કેયેન, ફ્રેન્ચ ગુઆનામાં વૈજ્ઞાનિક અભિયાનનું નેતૃત્વ કર્યું હતું અને ઇટાલિયન-ફ્રેન્ચ ખગોળશાસ્ત્રી જીઓવાન્ની કેસિની, જે પેરિસમાં રહ્યા હતા. તેઓએ શક્ય તેટલા જ સમયે મંગળનું અવલોકન કર્યું અને નજીકના તારાની તુલનામાં તેની સ્થિતિ નોંધી. અવલોકન કરેલ સ્થિતિ તફાવતની ગણતરી કરીને, કેયેનથી પેરિસનું અંતર જાણીને, માપન સમયે મંગળથી અંતરની ગણતરી કરવામાં આવે છે.
એકવાર પૂર્ણ થઈ ગયા પછી, કેપ્લર મોડેલનો સ્કેલ ઉપલબ્ધ થશે, જે આપણને સૌરમંડળમાં અન્ય તમામ અંતરની ગણતરી કરવાની મંજૂરી આપશે. કેસિનીએ સૂર્ય-પૃથ્વીનું અંતર 140 મિલિયન કિલોમીટરનું અનુમાન લગાવ્યું હતું, વાસ્તવિક આંકડા કરતા 9 મિલિયન કિલોમીટર ઓછા છે, પરંતુ પ્રથમ પ્રયાસના પરિણામો ખૂબ સારા હતા.
પાછળથી, ગ્રહોના લંબનનું વધુ ચોક્કસ માપન કરવામાં આવ્યું. શુક્ર પરના કેટલાક, જ્યાં તે પૃથ્વી અને સૂર્ય વચ્ચે બરાબર પસાર થાય છે, તે સૌર ડિસ્ક પર નાના શ્યામ વર્તુળ તરીકે જોઈ શકાય છે. આ સંક્રમણો 1761 અને 1769 માં થયા હતા. જો બે અલગ-અલગ વેધશાળાઓમાંથી તે ચકાસી શકાય છે કે શુક્રના સૌર ડિસ્ક સાથેના સંપર્કની ક્ષણ અને સોલાર ડિસ્કથી તેના અલગ થવાની ક્ષણ, એટલે કે, પરિવહનનો સમયગાળો એક વેધશાળાથી બીજી વેધશાળામાં અલગ છે. આ ફેરફારો અને બે વેધશાળાઓ વચ્ચેના અંતરને જાણીને શુક્રના લંબનની ગણતરી કરી શકાય છે. આ ડેટા દ્વારા તમે શુક્ર અને પછી સૂર્ય સુધીના અંતરની ગણતરી કરી શકો છો.
હું આશા રાખું છું કે આ માહિતી સાથે તમે લંબન શું છે અને તેની લાક્ષણિકતાઓ વિશે વધુ જાણી શકશો.