La parallax is the angular deviation of the apparent position of an object, depending on the chosen point of view. This has certain applications in the world of astronomy both to measure distances and to visualize celestial objects. Many people do not know what parallax is.
Therefore, in this article we are going to tell you what the parallax is, what its characteristics are and its importance.
what is parallax
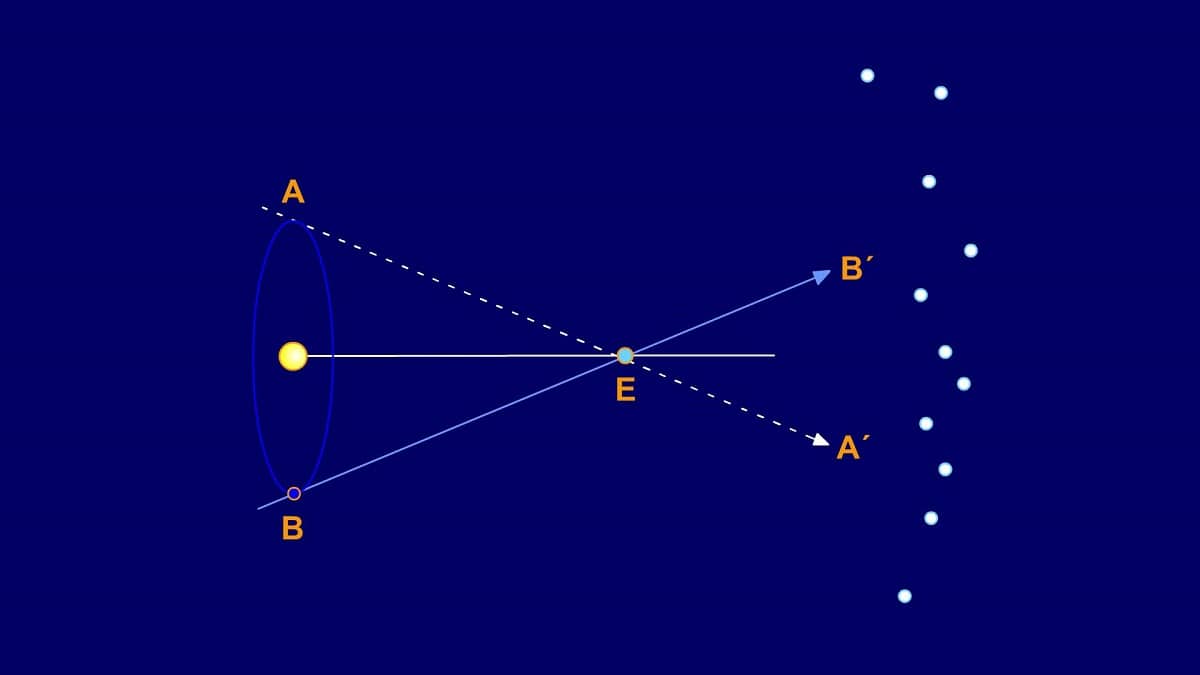
Parallax involves placing your fingers in front of your eyes. The background should not be uniform. Looking first with one eye and then with the other without moving the head or the finger, it can be seen that the position of the finger changes with respect to the background. If we bring our finger closer to the eye and look again with one eye and then with the other, the two finger positions on the background cover a larger portion.
This is because there are a few centimeters between the eyes, so the imaginary line connecting the fingers to one eye makes an angle with the imaginary line connecting the fingers to the other eye. If we extend these two imaginary lines to the bottom, we will have two points corresponding to the two different positions of the fingers.
The closer we place the finger to the eye, the greater the angle and the greater the apparent displacement. If the eyes were further apart, the angle formed by the two lines would increase more, so the apparent displacement of the finger from the background would be greater.
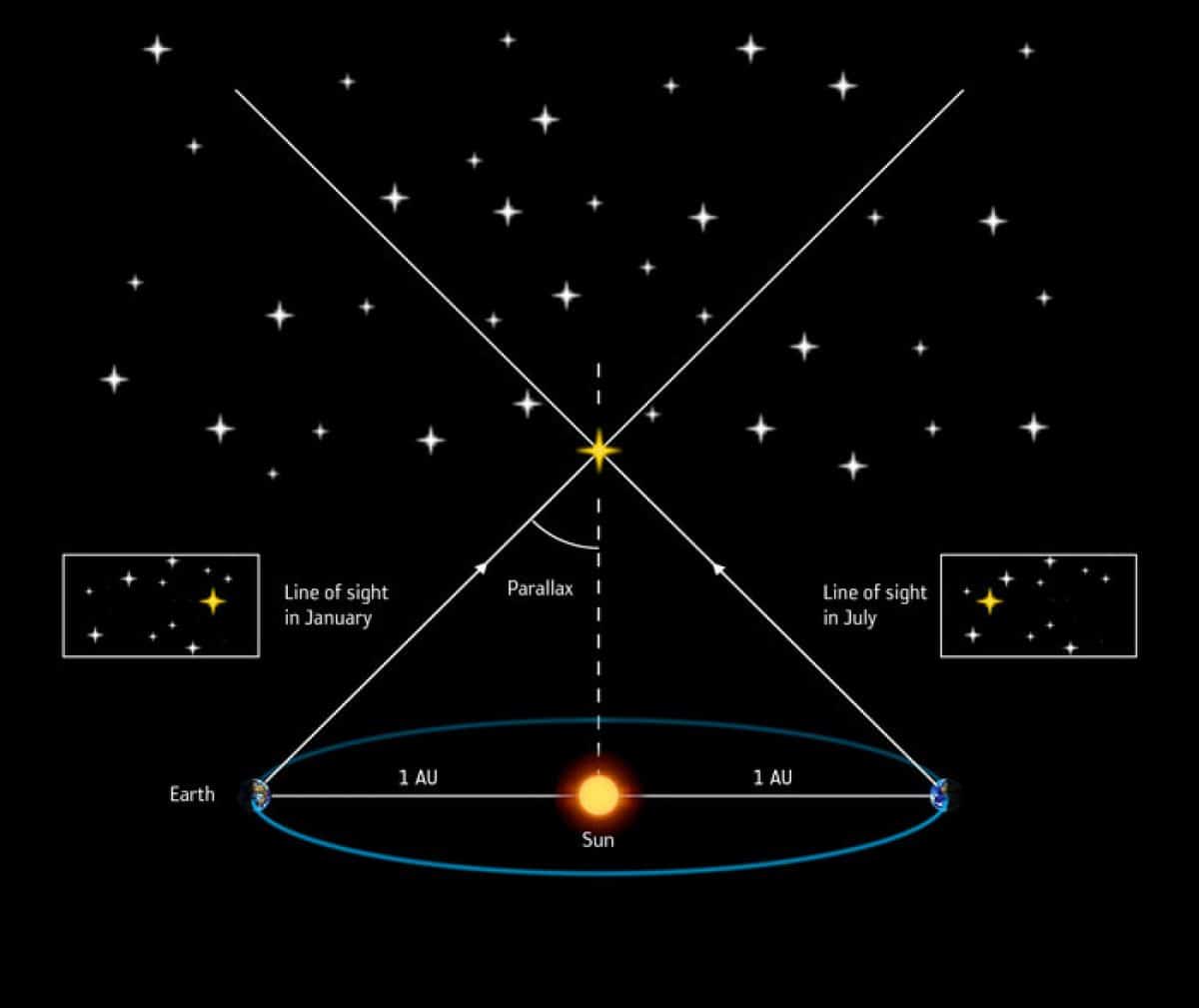
parallax in astronomy

This also applies to planets. In fact, the moon is so far away that we cannot tell any difference when we look at it with our eyes. But if we look at the Moon against the backdrop of a starry sky from two observatories hundreds of kilometers apart, we notice a few things. From the first observatory we would see an edge of the moon at a certain distance from a particular star, while at the second observatory the same edge would be at a different distance from the same star.
Knowing the apparent displacement of the Moon with respect to the starry background and the distance between the two observatories, this distance can be calculated with the help of trigonometry.
This experiment works perfectly because the apparent displacement of the Moon with respect to the background of the starry sky is very large when changing the position of the observer. Astronomers have normalized this offset to accommodate the situation in which one observer sees the moon on the horizon while the other is above it. The base of the triangle is equal to the radius of the earth, and the angle it makes with the vertex of the moon is the "horizontal parallax at the equator." Its value is 57,04 minutes of arc or 0,95 radians.
In fact, a considerable displacement, since it is equivalent to twice the apparent diameter of the full moon. This is a magnitude that can be measured with enough precision to get a good value for the distance to the Moon. This distance, calculated with the help of parallax, agrees very well with the figures obtained by the old method of shadows cast by the Earth during lunar eclipses.
Unfortunately, conditions in 1600 did not allow placing the observatory far enough, which, combined with the great distances at which the planets were discovered, made the apparent displacement against the background of the starry sky too small to be exact.
PREMIUM QUALITY
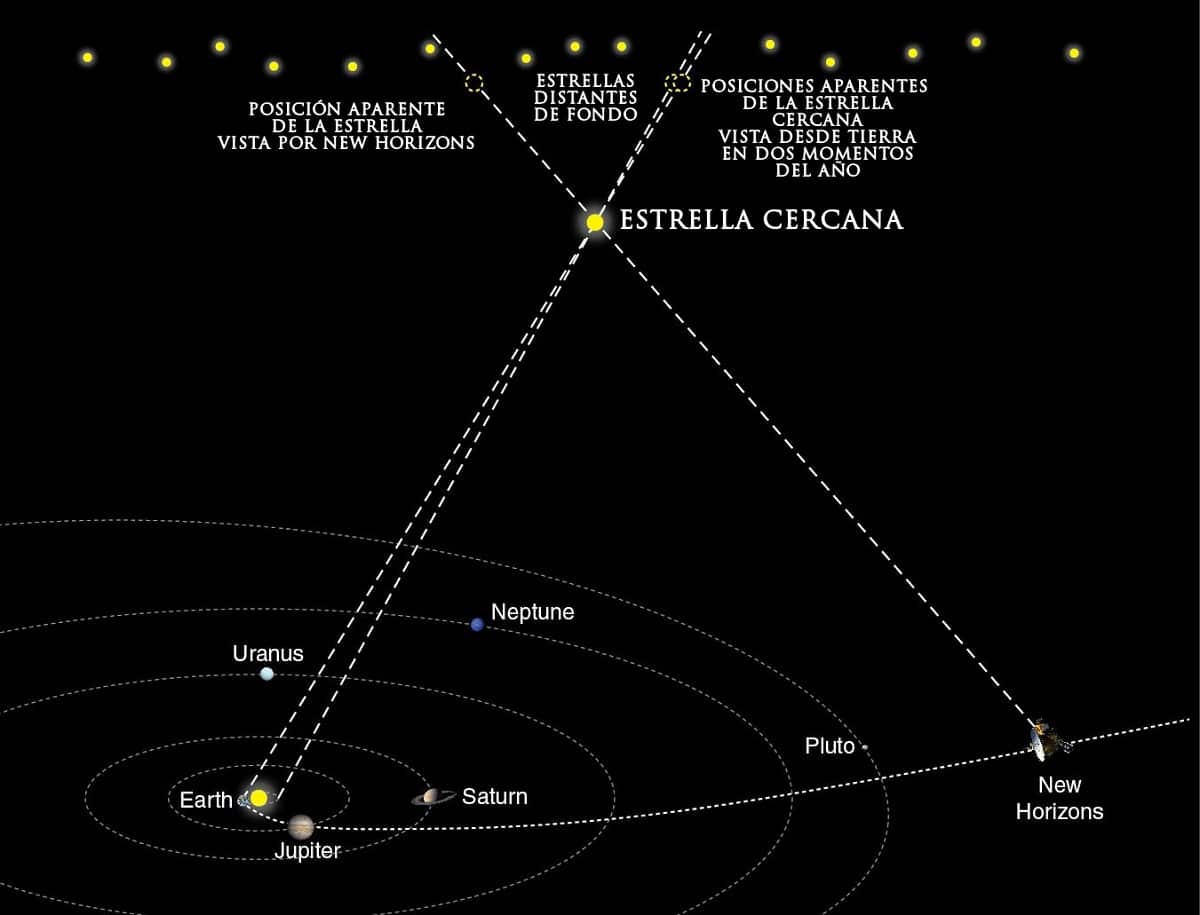
We can say that there are two types of parallax:
- Geocentric Parallax: When the radius used is the ground.
- Spiral Centroid or Annual Parallax: When the radius used is the Earth's orbit around the sun.
If we observe a star in January and June, the Earth will be in two relative positions in Earth's orbit. We can measure changes in the apparent position of the star. The greater the parallax, the closer that star is. For this, the parsec is used as the unit, which is defined as the reciprocal of the triangular parallax measured in seconds of arc.
parallax investigations
Later came the telescopes invented or modified by the Italian scientist Galileo Galilei. Telescopes can easily measure angular distances that cannot be detected with the naked eye.
The planets with the greatest parallax are the closest planets, namely Mars and Venus. Venus is so close to the sun during its closest pass that it cannot be observed except when it is visible against the background of the solar disk during its transit. Then, the only case where parallax is measured is Mars.
The first telescopic measurement of planetary parallax was made in 1671. The two observers were the French astronomer Jean Richel, who led the scientific expedition to Cayenne, French Guiana, and the Italian-French astronomer Giovanni Cassini, who remained in Paris. They observed Mars at the same time as possible and noted its position relative to the nearest star. By calculating the observed position difference, knowing the distance from Cayenne to Paris, the distance from Mars at the time of measurement is calculated.
Once completed, the scale of the Kepler model will be available, allowing us to calculate all other distances in the solar system. Cassini estimated the Sun-Earth distance at 140 million kilometers, 9 million kilometers less than the real figure, but the results of the first attempt were very good.
Later, more precise measurements of planetary parallax were made. Some on Venus, where it passes exactly between the Earth and the Sun, can be seen as a small dark circle on the solar disk. These transits occurred in 1761 and 1769. If from two different observatories it can be verified that the moment of contact of Venus with the solar disk and the moment of its separation from the solar disk, that is, the duration of the transit is different from one observatory to another. Knowing these changes and the distance between the two observatories, the parallax of Venus can be calculated. With these data you can calculate the distance to Venus and then to the Sun.
I hope that with this information you can learn more about what parallax is and its characteristics.